
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )

A. 4个 B.3个 C 2个 D. 1个
B 解:∵抛物线和x轴有两个交点,
∴b2﹣4ac>0,
∴4ac﹣b2<0,∴①正确;
∵对称轴是直线x=﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,
∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,
∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,
∴4a+c>2b,∴②错误;
∵把(1,0)代入抛 物线得:y=a+b+c<0,
物线得:y=a+b+c<0,
∴2a+2b+2c<0,
∵b=2a,
∴3b+2c<0,∴③正确;
∵抛物线的对称轴是直线x=﹣1,
∴y=a﹣b+c的值最大,
即把x=m(m≠﹣1)代入得:y=am2+bm+c<a﹣b+c,
∴am2+bm+b<a,
即m(am+b)+b<a,∴④正确;
即正确的有3个,


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
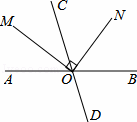
A. 35° B.45° C55° D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+ kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
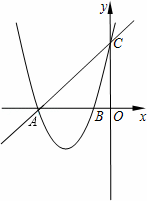
查看答案和解析>>
科目:初中数学 来源: 题型:
某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com