
分析 分式的值为负数则分式的分子与分母异号,然后列不等式或不等式组求解即可.
解答 解:(1)∵分式的值是负数,
∴1-3x>0.
解得:x<$\frac{1}{3}$.
∴当x$<\frac{1}{3}$时,分式$\frac{-2}{1-3x}$的值为负数;
(2)∵分式的值是负数,
∴3x-6<0,且x2≠0.
解得:x<2且x≠0.
∴当x<2且x≠0时,分式$\frac{3x-6}{{x}^{2}}$的值为负数;
(3)∵分式的值是负数,
∴$\left\{\begin{array}{l}{x-1>0}\\{x+2<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-1<0}\\{x+2>0}\end{array}\right.$
解得:-2<x<1.
∴当-2<x<1时,分式$\frac{x-1}{x+2}$的值为负数.
点评 本题主要考查的是分式的值,根据题意得到关于x的不等式或不等式组是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
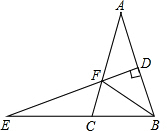 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?
如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com