
【题目】探究与应用
(提出问题)
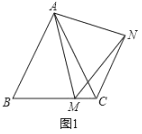
(1)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() 、
、![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
(类比探究)
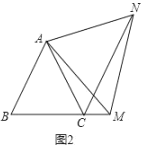
(2)如图2,在等边![]() 中,点
中,点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,(1)中结论
),其它条件不变,(1)中结论![]() 还成立吗?请说明理由.
还成立吗?请说明理由.
(拓展延伸)
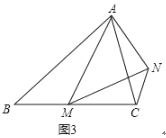
(3)如图3,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() 、
、![]() )连结
)连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使顶角
,使顶角![]() .连结
.连结![]() .试探究
.试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)见解析;(2)仍成立,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到![]() ,根据∠BAM=∠BAC-∠MAC,∠CAN=∠MAN-∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
,根据∠BAM=∠BAC-∠MAC,∠CAN=∠MAN-∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
(1)证明:∵![]() 、
、![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵在![]() 和
和![]() 中,
中,
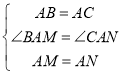 ,
,
∴![]() .
.
∴![]() .
.
(2)结论![]() 仍成立.理由如下:
仍成立.理由如下:
∵![]() 、
、![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵在![]() 和
和![]() 中,
中,
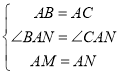 ,
,
∴![]() .
.
∴![]() .
.
(3)![]() .理由如下:
.理由如下:
∵![]() ,
,![]() 顶角
顶角![]() ,
,
∴底角![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①![]() =
=![]() ;②
;②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数为( )
.其中正确的个数为( )
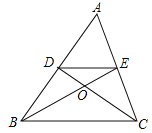
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为![]() 的篱笆,现一面利用墙(墙的最大可用长度
的篱笆,现一面利用墙(墙的最大可用长度![]() 为
为![]() )围成中间隔有一道篱笆的长方形花圃,设花圃的宽
)围成中间隔有一道篱笆的长方形花圃,设花圃的宽![]() 为
为![]() ,面积为
,面积为![]() .
.
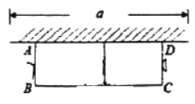
(1)求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)要围成面积为![]() 的花圃,
的花圃,![]() 的长是多少米?
的长是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
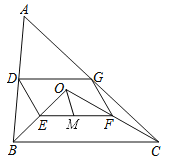
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
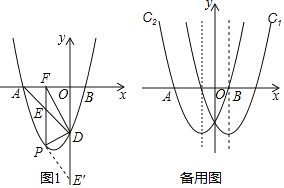
【题目】在同一直角坐标系中,抛物线C1:![]() 2
2![]() 与抛物线C2:
与抛物线C2:![]() 2
2![]() 关于
关于![]() 轴对称,C2与
轴对称,C2与![]() 轴交于A、B两点,其中点A在点B的左侧交y轴于点D.
轴交于A、B两点,其中点A在点B的左侧交y轴于点D.
(1)求A、B两点的坐标;
(2)对于抛物线C2:![]() 2
2![]() 在第三象限部分的一点P,作PF⊥
在第三象限部分的一点P,作PF⊥![]() 轴于F,交AD于点E,若E关于PD的对称点E′恰好落在
轴于F,交AD于点E,若E关于PD的对称点E′恰好落在![]() 轴上,求P点坐标;
轴上,求P点坐标;
(3)在抛物线C1上是否存在一点G,在抛物线C2上是否存在一点Q,使得以A、B、G、Q四点为顶点的四边形是平行四边形?若存在,求出G、Q两点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com