
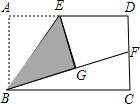
 如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.
如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$. 分析 连接EF,则AE=EG,HL可证明Rt△EGF≌Rt△EDF,根据全等三角形的性质得到GF=DF,设FC=x,BC=y,则有GF=x,AD=y.根据DC=2FC得到DF=x,DC=AB=BG=2x,BF=BG+GF=3x,然后利用勾股定理得到y与x之间关系,从而求得两条线段的比.
解答 解:连接EF,则∠EGF=∠D=90°.
∵点E是AD的中点,
∴由折叠的性质知,EG=ED
在Rt△EGF和Rt△EDF中,
$\left\{\begin{array}{l}{EG=ED}\\{EF=EF}\end{array}\right.$,
∴Rt△EGF≌Rt△EDF(HL).
∴GF=DF,
设FC=x,BC=y,则有GF=x,AD=y.
∵DC=2FC,
∴DF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x.
在Rt△BCF中,由勾股定理得:BC2+CF2=BF2,即y2+x2=(3x)2.
∴y=2$\sqrt{2}$x
∴$\frac{AD}{AB}$=$\frac{y}{2x}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | 0.45×106吨 | B. | 4.5×105吨 | C. | 45×104吨 | D. | 4.5×104吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
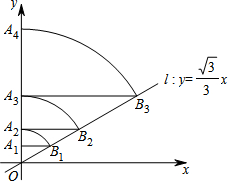 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=22016.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=22016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
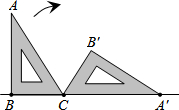 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=4,将△ABD沿对角线对折,得到△EBD(点E为点A的对应点),DE与BC交于点F,cos∠ADB=$\frac{3\sqrt{13}}{13}$,则EF=$\frac{5}{3}$.
如图,在矩形ABCD中,AB=4,将△ABD沿对角线对折,得到△EBD(点E为点A的对应点),DE与BC交于点F,cos∠ADB=$\frac{3\sqrt{13}}{13}$,则EF=$\frac{5}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
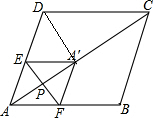 如图,在菱形ABCD中,AB=5,AC=8,P为AC上一动点,过P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在对角线AC上的点A′处,当△A′CD为直角三角形时,AP的长为2或$\frac{7}{8}$.
如图,在菱形ABCD中,AB=5,AC=8,P为AC上一动点,过P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在对角线AC上的点A′处,当△A′CD为直角三角形时,AP的长为2或$\frac{7}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com