Question

已知△ABC的各边之比是2：5：6，与其相似的另一个△A'B'C'的最长边为18cm，则它的最短边的长是________．

Answer 1

6cm
分析：由△ABC的各边之比是2：5：6，△A′B′C′∽△ABC，可得△A′B′C′的各边之比是2：5：6，又由△A′B′C′的最长边为18cm，即可求得△A′B′C′的最短边的长．
解答：∵△ABC的各边之比是2：5：6，
∴△A′B′C′的各边之比是2：5：6，
设△A′B′C′的最短边的长为xcm，
∵与其相似的另一个△A′B′C′的最长边为18cm，
∴，
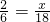
解得：x=6，
∴△A′B′C′的最短边的长为6cm．
故答案为：6cm．
点评：此题考查了相似三角形的性质．注意相似三角形的对应边成比例定理的应用．