
【题目】我们定义:两边平方和等于第三边平方的两倍的三角形叫做“奇异三角形”.
(1)根据“奇异三角形”的定义,请你判断命题:“等边三角形一定是奇异三角形” 是 命题.(填写“真命题、假命题”)
(2)在RtΔABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若RtΔABC是“奇异三角形”,则a:b:c= .
(3)如图,在四边形ACBD中,∠ACB=∠ADB=90°,AD=BD,若在四边形ACBD内存在点E使得AE=AD,CB=CE.
①求证:ΔACE是“奇异三角形”;
②当ΔACE是直角三角形时,且AC=![]() ,求线段AB 的长.
,求线段AB 的长.

【答案】(1)真;(2)![]() ;(3)①证明见解析;②
;(3)①证明见解析;②![]() 或
或![]() .
.
【解析】
(1)等边三角形三边长相等,可判断符合“奇异三角形”定义;
(2)先根据勾股定理,可得出a、b、c的关系,再根据“奇异三角形”可得出a、b、c的关系,化简可求得a:b:c的值;
(3)①先在Rt△ABD和Rt△ACB中,利用勾股定理得出边的关系,再利用边长之间的转化,推导得出△ACE是“奇异三角形”;
②设BC=a,AD=b,根据“奇异三角形”ACE,可得出a、b之间的关系,在Rt△ACE中,利用勾股定理也可得a、b的关系式,从而求出a、b的值,进而得出AB的长.
(1)设等边三角形的边长为a
则两边平方和=![]() ,第三边平方的两倍为:2
,第三边平方的两倍为:2![]()
∵![]() 2
2![]()
∴结论为:真;
(2)∵△ABC是直角三角形,∴![]()
∵△ABC是“奇异三角形”,∴![]()
化简得:![]() ,
,![]()
解得b=![]() ,c=
,c=![]()
∴a:b:c=![]() ;
;
(3) ①证明:
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是“奇异三角形”
是“奇异三角形”
②设![]() ,
,![]()
![]()
![]()
由①得:![]()
![]()
![]() 为直角三角形
为直角三角形
![]() 或
或![]()
当![]() 时
时
![]()
![]()
由上述得![]()
![]()
![]()
当![]() 时
时
![]()
![]()
由上述得![]()
![]()
![]()
![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=![]() EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省空间,家里的饭碗一般是竖直摆放的,如果![]() 只饭碗(形状、大小相同)竖直摆放的高度为
只饭碗(形状、大小相同)竖直摆放的高度为![]() 只饭碗竖直摆放的高度为
只饭碗竖直摆放的高度为![]() .如图所示,小颖家的碗橱每格的高度为
.如图所示,小颖家的碗橱每格的高度为![]() 则一摞碗竖直放人橱柜时,每格最多能放________________________.
则一摞碗竖直放人橱柜时,每格最多能放________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
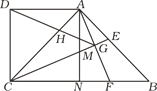
【题目】如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若|x+2y-10|+|2x-y|=0,试分别求出1秒钟后△AOB的面积;
(2)如图2,所示,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图3所示,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,设∠AGH=α,∠BGC=β,试探究出α和β满足的数量关系并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,
∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别为多少?

(2)(生活应用题)某公司对一批某一品牌的衬衣的质量抽检结果如下表:

①从这批衬衣中任抽1件是次品的概率约为多少?
②如果销售这批衬衣600件,那么至少需要准备多少件正品衬衣供买到次品的顾客调换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.

(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
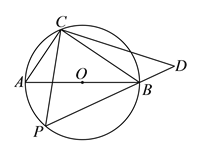
【题目】如图,圆![]() 的直径为
的直径为![]() ,在圆
,在圆![]() 上位于直径
上位于直径![]() 的异侧有定点
的异侧有定点![]() 和动点
和动点![]() ,已知
,已知![]() ,点
,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 的延长线于
的延长线于![]() 点.
点.
(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 运动到
运动到![]() 弧中点时,求
弧中点时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1个足球和1个篮球共需150元,购买2个足球和1个篮球共需200元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共50个,总费用不超过4000元,最多可以买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com