
【题目】通过对下面数学模型的研究学习,解决下列问题:
(模型呈现)
(1)如图1,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .由
.由![]() ,得
,得![]() .又
.又![]() ,可以推理得到
,可以推理得到![]() .进而得到
.进而得到![]() _____,
_____,![]() _____.我们把这个数学模型称为“
_____.我们把这个数学模型称为“![]() 字”模型或“一线三等角”模型;
字”模型或“一线三等角”模型;
(模型应用)
(2)①如图2,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .求证:点
.求证:点![]() 是
是![]() 的中点.
的中点.
②如图3,在平面直角坐标系![]() 中,点
中,点![]() 为平面内任一点,点
为平面内任一点,点![]() 的坐标为
的坐标为![]() .若
.若![]() 是以
是以![]() 为斜边的等腰直角三角形,请直接写出点
为斜边的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.

科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依此规律,得到Rt△B2018A2019B2019,则点B2019的纵坐标为________.
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依此规律,得到Rt△B2018A2019B2019,则点B2019的纵坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以∠C为直角的直角三角形,且BC=1,AC=![]() ,圆O是△ABC的外接圆,过△ABC的内角∠C作角平分线交AB于点D,交圆O与点E,连接AE,
,圆O是△ABC的外接圆,过△ABC的内角∠C作角平分线交AB于点D,交圆O与点E,连接AE,
(1)求AE的长.
(2)求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=|x|-2的图象特征进行了探究,探究过程如下:
⑴自变量x的取值范围是全体实数,x与y的几组对应值如下:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中,m= ,n= .
⑵根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象;

⑶观察函数图象,写出一条特征: .
查看答案和解析>>
科目:初中数学 来源: 题型:
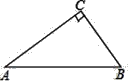
【题目】如图,在直角三角形ABC中,
(1)过点A作AB的垂线与∠B的平分线相交于点D
(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠A=30°,AB=2,则△ABD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3过等腰Rt△BOC的两顶点B、C,且与x轴交于点A(﹣1,0).
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线BC相交于点M,点N为x轴上一点,当以M,N,B为顶点的三角形与△ABC相似时,求BN的长度;
(3)P为线段BC上方的抛物线上的一个动点,P到直线BC的距离是否存在最大值?若存在,请求出这个最大值的大小以及此时点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委组织“阳光助残”献爱心捐款活动,九年级(2)班学生捐款如表:
捐款金额(元) | 5 | 10 | 15 | 20 |
人数(人) | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是( )
A. 10元,15元 B. 15元,15元 C. 10元,20元 D. 16元,17元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,OC OD,OC OD ,DC 的延长线交 y 轴正半轴上点 B ,过点C 作CA BD 交 x 轴负半轴于点A .

(1)如图1,求证:OAOB
(2)如图1,连AD,作OM ∥AC交AD于点M,求证: BC 2OM
(3)如图2,点E为OC 的延长线上一点,连DE,过点D作DFDE且DF DE ,连CF 交 DO 的延长线于点G 若OG 4,求CE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com