练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
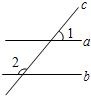
    如图，直线a，b被直线c所截，下列说法正确的是（　　）
    A、当∠1=∠2时，a∥b
    B、当a∥b时，∠1=∠2
    C、当a∥b时，∠1+∠2=90°
    D、当a∥b时，∠1+∠2=180°
    考点：平行线的性质,平行线的判定
    专题：
    分析：根据平行线的性质，两直线平行，同旁内角互补以及对顶角的性质即可判断．
    解答：解：∠1=∠2时，∠2=∠3，同旁内角相等，a∥b不一定成立，选项A错误；
    当a∥b时，∠2+∠3=180°，而∠1=∠3，则∠1+∠2=180°，故D正确．
    故选D．
    点评：本题考查了平行线的性质，对顶角相等，是一道较为简单的题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知正比例函数y=（3k-1）x．若y随x的增大而减小，则k的取值范围是（　　）
    A、k＜0
    B、k＞0
    C、k＜
    1
    3
    D、k＞
    1
    3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    （1）
    x=3y-5
    3y=8-2x

    （2）
    5x2-4y2=20
    		15
    x-2y=2
    		15

    （3）x2+4x-2=0
    （4）
    3
    x-1
    -
    x+2
    x(x-1)
    =0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，AB=AC，将线段AC绕着点C逆时针旋转得到线段CD，旋转角为α，且0°＜α＜180°，连接AD、BD．
    （1）如图1，当∠BAC=100°，α=60°时，∠CBD的大小为
     
    ；
    （2）如图2，当∠BAC=100°，α=20°时，求∠CBD的大小；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，正方形ABCD各顶点均在正方形EFGH的各边上（GB＜BF），且两正方形面积分别为25和49，则tan∠ABF=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知矩形ABCD和点P，当点P在图1中的位置时，则有结论：S△PBC=S△PAC+S△PCD
    理由：过点P作EF垂直BC，分别交AD、BC于E、F两点．
    ∵S△PBC+S△PAD=
    1
    2
    BC•PF+
    1
    2
    AD•PE=
    1
    2
    BC（PF+PE）=
    1
    2
    BC•EF=
    1
    2
    S矩形ABCD．
    （1）请补全以上证明过程．
    （2）请你参考上述信息，当点P分别在图1、图2中的位置时，S△PBC、S△PAC、SPCD又有怎样的数量关系？请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

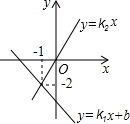    同一平面直角坐标系中，一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示，则关于x的方程k1x+b=k2x的解为（　　）
    A、x=0B、x=-1
    C、x=-2D、x=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：a÷
    1
    b
    •b•c÷
    1
    c
    ÷
    1
    d
    •d=（　　）
    A、a
    B、
    a
    b2c2d2
    C、
    1
    a
    D、ab2c2d

    查看答案和解析>>

    科目：初中数学 来源： 题型：

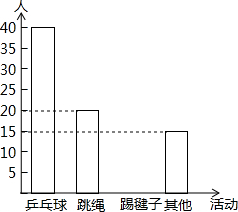    某校为开展“阳光体育”运动，丰富学生课间自由活动内容，随机选取了本校100名学生进行调查，调查的内容是：你最喜欢的自由活动项目是什么？并将收集到的数据整理，绘出了如图所示的统计图．
    （1）学校采用的调查方法是
     
    ．
    （2）求“踢毽子”的人数，并在下图中将“踢毽子”部分的条形图补充完整．
    （3）若该校有1800名学生，请估计喜欢“跳绳”的学生人数．

    查看答案和解析>>

    同步练习册答案