
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌНЋЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1 ЃЌ а§зЊНЧЮЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЃЌСЌНгAC1ЁЂBD1 ЃЌ AC1гыBD1НЛгкЕуPЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЫФБпаЮABCDЪЧе§ЗНаЮЃЎ
ЂйЧѓжЄЃКЁїAOC1ЁеЁїBOD1 ЃЎ
ЂкЧыжБНгаДГіAC1 гыBD1ЕФЮЛжУЙиЯЕЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєЫФБпаЮABCDЪЧСтаЮЃЌAC=5ЃЌBD=7ЃЌЩшAC1=kBD1 ЃЎ ХаЖЯAC1гыBD1ЕФЮЛжУЙиЯЕЃЌЫЕУїРэгЩЃЌВЂЧѓГіkЕФжЕЃЎ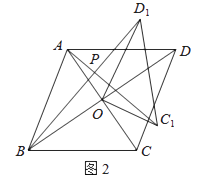
ЃЈ3ЃЉШчЭМ3ЃЌШєЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌAC=5ЃЌBD=10ЃЌСЌНгDD1 ЃЌ ЩшAC1=kBD1 ЃЎ ЧыжБНгаДГіkЕФжЕКЭAC12+ЃЈkDD1ЃЉ2ЕФжЕЃЎ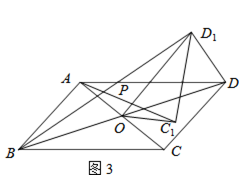
ЁОД№АИЁП
ЃЈ1ЃЉ
ЂйжЄУїЃКШчЭМ1ЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрOC=OA=OD=OBЃЌACЁЭBDЃЌ
ЁрЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1ЃЌ
ЁрOC1=OD1ЃЌЁЯAOC1=ЁЯBOD1=90Ёу+ЁЯAOD1ЃЌ
дкЁїAOC1КЭЁїBOD1жа
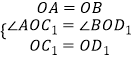 ЃЌ
ЃЌ
ЁрЁїAOC1ЁеЁїBOD1ЃЈSASЃЉЃЛ
ЂкAC1ЁЭBD1ЃЛ
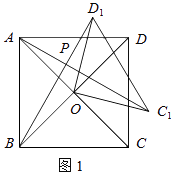
ЃЈ2ЃЉ
НтЃКAC1ЁЭBD1ЃЎ
РэгЩШчЯТЃКШчЭМ2ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрOC=OA= ![]() ACЃЌOD=OB=
ACЃЌOD=OB= ![]() BDЃЌACЁЭBDЃЌ
BDЃЌACЁЭBDЃЌ
ЁрЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1ЃЌ
ЁрOC1=OAЃЌOD1=OBЃЌЁЯAOC1=ЁЯBOD1ЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁрЁїAOC1ЁзЁїBOD1ЃЌ
ЁрЁЯOAC1=ЁЯOBD1ЃЌ
гжЁпЁЯAOB=90ЁуЃЌ
ЁрЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌ
ЁрЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌ
ЁрЁЯAPB=90Ёу
ЁрAC1ЁЭBD1ЃЛ
ЁпЁїAOC1ЁзЁїBOD1ЃЌ
Ёр ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
Ёрk= ![]() ЃЛ
ЃЛ
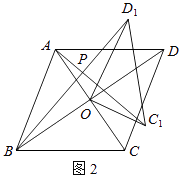
ЃЈ3ЃЉ
НтЃКШчЭМ3ЃЌгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1ЃЌ
Ёр ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
Ёрk= ![]() ЃЛ
ЃЛ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOD1=ODЃЌ
ЖјOD=OBЃЌ
ЁрOD1=OB=ODЃЌ
ЁрЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌ
дкRtЁїBDD1жаЃЌ
BD12+DD12=BD2=100ЃЌ
ЁрЃЈ2AC1ЃЉ2+DD12=100ЃЌ
ЁрAC12+ЃЈkDD1ЃЉ2=25ЃЎ
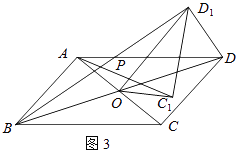
ЁОНтЮіЁПЃЈ1ЃЉЂйШчЭМ1ЃЌИљОне§ЗНаЮЕФаджЪЕУOC=OA=OD=OBЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OD1 ЃЌ РћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ ШЛКѓИљОнЁАSASЁБПЩжЄУїЁїAOC1ЁеЁїBOD1ЃЛЂкгЩЁЯAOB=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌЫљвдЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЫљвдAC1ЁЭBD1ЃЛЃЈ2ЃЉШчЭМ2ЃЌИљОнСтаЮЕФаджЪЕУOC=OA= ![]() ACЃЌOD=OB=
ACЃЌOD=OB= ![]() BDЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OAЃЌOD1=OBЃЌРћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ МгЩЯ
BDЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OAЃЌOD1=OBЃЌРћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ МгЩЯ ![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЕУЕНЁїAOC1ЁзЁїBOD1 ЃЌ ЕУЕНЁЯOAC1=ЁЯOBD1 ЃЌ гЩЁЯAOB=90ЁуЕУЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЃЌЫљвдAC1ЁЭBD1ЃЛШЛКѓИљОнЯрЫЦБШЕУЕН
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЕУЕНЁїAOC1ЁзЁїBOD1 ЃЌ ЕУЕНЁЯOAC1=ЁЯOBD1 ЃЌ гЩЁЯAOB=90ЁуЕУЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЃЌЫљвдAC1ЁЭBD1ЃЛШЛКѓИљОнЯрЫЦБШЕУЕН ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌЫљвдk=
ЃЌЫљвдk= ![]() ЃЛЃЈ3ЃЉгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1 ЃЌ дђ
ЃЛЃЈ3ЃЉгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1 ЃЌ дђ ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌЫљвдk=
ЃЌЫљвдk= ![]() ЃЛИљОна§зЊЕФаджЪЕУOD1=ODЃЌИљОнЦНааЫФБпаЮЕФаджЪЕУOD=OBЃЌдђOD1=OB=ODЃЌгкЪЧПЩХаЖЯЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕУBD12+DD12=BD2=100ЃЌЫљвдЃЈ2AC1ЃЉ2+DD12=100ЃЌгкЪЧгаAC12+ЃЈkDD1ЃЉ2=25ЃЎ
ЃЛИљОна§зЊЕФаджЪЕУOD1=ODЃЌИљОнЦНааЫФБпаЮЕФаджЪЕУOD=OBЃЌдђOD1=OB=ODЃЌгкЪЧПЩХаЖЯЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕУBD12+DD12=BD2=100ЃЌЫљвдЃЈ2AC1ЃЉ2+DD12=100ЃЌгкЪЧгаAC12+ЃЈkDD1ЃЉ2=25ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћзЈТєЕъЯњЪлгЃЬвЃЌЦфНјМлЮЊУПЧЇПЫ![]() дЊЃЌАДУПЧЇПЫ
дЊЃЌАДУПЧЇПЫ![]() дЊГіЪлЃЌЦНОљУПЬьПЩЪлГі
дЊГіЪлЃЌЦНОљУПЬьПЩЪлГі![]() ЧЇПЫЃЌКѓРДОЙ§ЪаГЁЕїВщЗЂЯжЃЌЕЅМлУПЧЇПЫНЕЕЭ
ЧЇПЫЃЌКѓРДОЙ§ЪаГЁЕїВщЗЂЯжЃЌЕЅМлУПЧЇПЫНЕЕЭ![]() дЊЃЌдђЦНОљУПЬьЕФЯњЪлПЩдіМг
дЊЃЌдђЦНОљУПЬьЕФЯњЪлПЩдіМг![]() ЧЇПЫЃЌШєИУзЈТєЕъЯњЪлетжжгЃЬввЊЯыЦНОљУПЬьЛёРћ
ЧЇПЫЃЌШєИУзЈТєЕъЯњЪлетжжгЃЬввЊЯыЦНОљУПЬьЛёРћ![]() дЊЃЌЧыЛиД№ЃК
дЊЃЌЧыЛиД№ЃК
ЃЈ![]() ЃЉУПЧЇПЫгЃЬвгІНЕМлЖрЩйдЊЃП
ЃЉУПЧЇПЫгЃЬвгІНЕМлЖрЩйдЊЃП
ЃЈ![]() ЃЉдкЦНОљУПЬьЛёРћВЛБфЕФЧщПіЯТЃЌЮЊОЁПЩФмШУРћгкЙЫПЭЃЌгЎЕУЪаГЁЃЌИУЕъгІАДдЪлМлЕФМИелГіЪлЃП
ЃЉдкЦНОљУПЬьЛёРћВЛБфЕФЧщПіЯТЃЌЮЊОЁПЩФмШУРћгкЙЫПЭЃЌгЎЕУЪаГЁЃЌИУЕъгІАДдЪлМлЕФМИелГіЪлЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌвд
ЃЌвд![]() ЕуЮЊЖЅЕуЁЂ
ЕуЮЊЖЅЕуЁЂ![]() ЮЊбќдкЕкШ§ЯѓЯозїЕШбќ
ЮЊбќдкЕкШ§ЯѓЯозїЕШбќ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓ
ЃЉЧѓ![]() ЕуЕФзјБъЃЎ
ЕуЕФзјБъЃЎ
ЃЈ![]() ЃЉШчЭМ
ЃЉШчЭМ![]() ЃЌ
ЃЌ ![]() ЮЊ
ЮЊ![]() жсИКАыжсЩЯвЛИіЖЏЕуЃЌЕБ
жсИКАыжсЩЯвЛИіЖЏЕуЃЌЕБ![]() Еуби
Еуби![]() жсИКАыжсЯђЯТдЫЖЏЪБЃЌвд
жсИКАыжсЯђЯТдЫЖЏЪБЃЌвд![]() ЮЊЖЅЕуЃЌ
ЮЊЖЅЕуЃЌ ![]() ЮЊбќзїЕШбќ
ЮЊбќзїЕШбќ![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() жсгк
жсгк![]() ЕуЃЌЧѓ
ЕуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкдВаФНЧЮЊ90ЁуЕФЩШаЮOABжаЃЌАыОЖOA=2cmЃЌCЮЊ ![]() ЕФжаЕуЃЌDЁЂEЗжБ№ЪЧOAЁЂOBЕФжаЕуЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊcm2 ЃЎ
ЕФжаЕуЃЌDЁЂEЗжБ№ЪЧOAЁЂOBЕФжаЕуЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊcm2 ЃЎ 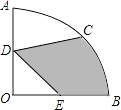
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЮCDЃЌFЮЊCDЩЯвЛЕуЃЌЁЯEFD=60ЁуЃЌЁЯAEC=2ЁЯCEFЃЌШє6ЁуЃМЁЯBAEЃМ15ЁуЃЌЁЯCЕФЖШЪ§ЮЊећЪ§ЃЌдђЁЯCЕФЖШЪ§ЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛЬѕжБЯпгыЗДБШР§КЏЪ§y= ![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкСНЕуAЁЂBЃЌгыxжсНЛгкЕуCЃЌЧвЕуBЪЧACЕФжаЕуЃЌЗжБ№Й§СНЕуAЁЂBзїxжсЕФЦНааЯпЃЌгыЗДБШР§КЏЪ§y=
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкСНЕуAЁЂBЃЌгыxжсНЛгкЕуCЃЌЧвЕуBЪЧACЕФжаЕуЃЌЗжБ№Й§СНЕуAЁЂBзїxжсЕФЦНааЯпЃЌгыЗДБШР§КЏЪ§y= ![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкСНЕуDЁЂEЃЌСЌНгDEЃЌдђЫФБпаЮABEDЕФУцЛ§ЮЊЃЈ ЃЉ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкСНЕуDЁЂEЃЌСЌНгDEЃЌдђЫФБпаЮABEDЕФУцЛ§ЮЊЃЈ ЃЉ 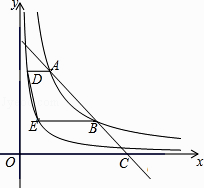
A.4
B.![]()
C.5
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌЁЯAЃЌЁЯBЃЌЁЯCЕФЖдБпЗжБ№ЮЊaЁЂbЁЂcЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ
AЃЎШчЙћЁЯCЃЁЯBЃНЁЯAЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЛ
BЃЎШчЙћ![]() ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЛ
ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЛ
CЃЎШчЙћЃЈcЃЋaЃЉЃЈ cЃaЃЉЃН![]() ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЛ
ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЛ
DЃЎШчЙћЁЯAЃКЁЯBЃКЁЯCЃН3ЃК2ЃК5ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЌЧвЁЯCЃН90ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃЈ2a+1ЃЉ2ЉЃЈ2a+1ЃЉЃЈЉ1+2aЃЉЃЛ
ЃЈ2ЃЉгУГЫЗЈЙЋЪНМЦЫуЃК20022Љ2001ЁС2003ЃЛ
ЃЈ3ЃЉНтВЛЕШЪНзщЃК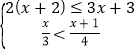 ЃЌВЂАбНтМЏдкЪ§жсЩЯБэЪОГіРДЃЛ
ЃЌВЂАбНтМЏдкЪ§жсЩЯБэЪОГіРДЃЛ
ЃЈ4ЃЉНтЗНГЬзщЃК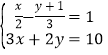 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy1=aЃЈx+2ЃЉ2-3гыy2= ![]() ЃЈx-3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЃЈx-3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЂйЮоТлxШЁКЮжЕЃЌy2ЕФжЕзмЪЧе§Ъ§ЃЛЂкa=1ЃЛЂлЕБx=0ЪБЃЌy2-y1=4ЃЛЂм2AB=3ACЃЛЦфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ
A.ЂйЂк
B.ЂкЂл
C.ЂлЂм
D.ЂйЂм
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com