
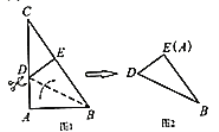
【题目】在三角形纸片![]() 中,
中,![]() ,
,![]() ,
,![]() .将该纸片沿过点
.将该纸片沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在斜边
落在斜边![]() 上的一点
上的一点![]() 处,折痕记为
处,折痕记为![]() (如图1),剪去
(如图1),剪去![]() 后得到双层
后得到双层![]() (如图2),再沿着边
(如图2),再沿着边![]() 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为__________cm.
某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为__________cm.
【答案】40或![]()
【解析】
解直角三角形得到AB=![]() ,CB=
,CB=![]() ,在Rt△CDE中根据勾股定理列方程求得DE=10.然后分两种情况求解,如图1,当ED=EF时,如图2,当ED=EF时.
,在Rt△CDE中根据勾股定理列方程求得DE=10.然后分两种情况求解,如图1,当ED=EF时,如图2,当ED=EF时.
解:如图1中,
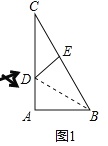
∵∠A=90°,∠C=30°,AC=30cm,
∴AB=BE=30tan30°=![]() ,CB=
,CB=![]() ,
,
∴CE=BC-BE=BC-AB=![]() cm.
cm.
设AD=DE=x cm,在Rt△CDE中,
(30-x)2=x2+(![]() )2,
)2,
∴x=10,
∴DE=10 cm,
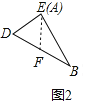
①如图2中,当ED=EF时,沿着直线EF将双层三角形剪开,展开后的平面图形中有一个是平行四边形,且是菱形,此时周长=4DE=4×10=40(cm);
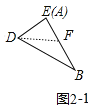
②如图2-1中,当FD=FB时,沿着直线DF将双层三角形剪开,展开后的平面图形中有一个是平行四边形,且是菱形,
∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∴∠DBE=30°,
∴∠BDF=30°,
∴∠DFE=60°,
∴DF=![]() =
=![]() cm,
cm,
此时周长=4DF=4×![]() cm,
cm,
综上所述,满足条件的平行四边形的周长为40cm或![]() cm,
cm,
故答案为为40或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
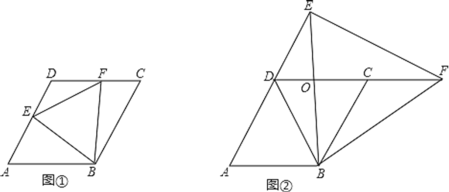
【题目】已知在边长为4的菱形ABCD中,∠EBF=∠A=60°,
(1)如图①,当点E、F分别在线段AD、DC上,
①判断△EBF的形状,并说明理由;
②若四边形ABFD的面积为7![]() ,求DE的长;
,求DE的长;
(2)如图②,当点E、F分别在线段AD、DC的延长线上,BE与DC交于点O,设△BOF的面积为S1,△EOD的面积为S2,则S1-S2的值是否为定值,如果是,请求出定值:如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
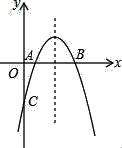
【题目】已知:如图所示,抛物线y=﹣x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)
(1)求抛物线的表达式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
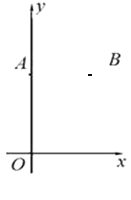
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:
①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形![]() 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中正确的语句有( )
的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中正确的语句有( )
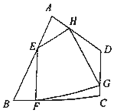
①当![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为菱形
为菱形
②当![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为矩形
为矩形
③当![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 可以为平行四边形
可以为平行四边形
④当![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 不可能为菱形
不可能为菱形
A.1句B.2句C.3句D.4句
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
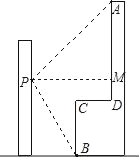
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
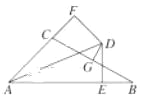
A. 6 B. 3 C. 2 D. 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践
如图①,![]() ,垂足分别为点
,垂足分别为点![]() ,
,![]() .
.
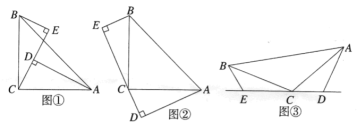
(1)求![]() 的长;
的长;
(2)将![]() 所在直线旋转到
所在直线旋转到![]() 的外部,如图②,猜想
的外部,如图②,猜想![]() 之间的数量关系,直接写出结论,不需证明;
之间的数量关系,直接写出结论,不需证明;
(3)如图③,将图①中的条件改为:在![]() 中,
中,![]() 三点在同一直线上,并且
三点在同一直线上,并且![]() ,其中
,其中![]() 为任意钝角.猜想
为任意钝角.猜想![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第8个正△A8B8C8的面积是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com