
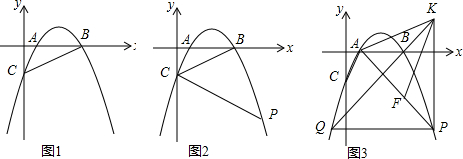
分析 (1)根据三角形的面积,可得C点的纵坐标,根据待定系数法,可得答案;
(2)根据相似三角形的判定与性质,可得答案;
(3)①根据等式的性质,可得∠HAP=∠HPA,根据等腰三角形的判定,可得PA=HA,可得答案;
②根据全等三角形的判定与性质,可得HK.根据等腰直角三角形的判定与性质,可得NQ与KN的关系,根据平行于x轴直线上两点间的距离是较大的横坐标减较小的横坐标,可得答案.
解答 解:(1)∵当y=0时,ax2-5ax+4a=0
解得 x1=1,x2=4,
∴A(1,0),B(4,0)
∴AB=3
由S△ABC$\frac{1}{2}$AB•|yC|=6,可得|yC|=OC=4,即C(0,-4),
将C点代入,得
a=-1
∴解析式为y=-x2+5x-4;
(2)过点C作CD∥x轴,过点P作PD⊥CD于点D,如图1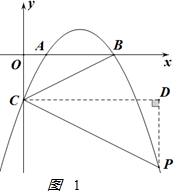 ,
,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC
∴∠PCD=∠ABC,∠PDC=∠BOC,
∴△PCD∽△CBO,
∴tan∠ABC=tan∠DCP
∴$\frac{OC}{OB}$=$\frac{DP}{CD}$,
设点P(t,at2-5at+4a)
DP=4a-(at2-5at+4a)=-at2+5at
∴$\frac{-a{t}^{2}+5at}{t}$=$\frac{-4a}{4}$
∴t=6
∴点P 的横坐标为6;
(3)①∵AK=FK
∴∠KAF=∠KFA
又∵∠KAH=∠FKP
∴∠HAP=∠HPA
∴HP=HA
由(2)知P 的横坐标为6,
∴P(6,10a)
∴HP=-10a
又∵HA=HO-AO=6-1=5
∴-10a=5
∴a=-$\frac{1}{2}$
∴抛物线的解析式为 y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
②过点F作FG⊥PK于点G,则Rt△PFG是等腰直角三角形如图2 ,
,
∵PF=-4$\sqrt{2}$a=2$\sqrt{2}$
∴FG=2
在△AKH和△KFG中,
$\left\{\begin{array}{l}{∠KAH=∠FKG}\\{∠AHK=∠KGF}\\{AK=FK}\end{array}\right.$
∴△AKH≌△KFG(AAS)
∴HK=FG=2
∴点K(6,2)
∵BH=KH=2
∴∠BKH=45°
过点Q作QN⊥PK于点N,则KN=QN ,
,
设点Q(t,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2),则N(6,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2)
∴QN=6-t
NK=2+$\frac{1}{2}$t2-$\frac{5}{2}$t+2=$\frac{1}{2}$t2-$\frac{5}{2}$t+2=$\frac{1}{2}$t2-$\frac{5}{2}$t+4
由KN=QN
得6-t=$\frac{1}{2}$t2-$\frac{5}{2}$t+4
解的t1=-1,t2=4(舍)
∴Q(-1,-5).
∵P(6,-5)
∴PQ∥x 轴,
∴QP=7.
点评 本题考查了二次函数综合题,解(1)的关键是利用三角形的面积的出C点坐标;解(2)的关键是利用相似三角形的判定与性质得出$\frac{-a{t}^{2}+5at}{t}$=$\frac{-4a}{4}$,解(3)①的关键是等腰三角形的判定得出PA=HA,解②的关键是;利用等腰直角三角形的判定与性质,可得NQ与KN的关系,又利用了平行于x轴直线上两点间的距离是较大的横坐标减较小的横坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.
如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
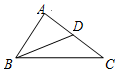 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com