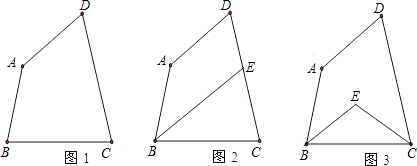
½ā“š£ŗ½ā£ŗ£Ø1£©CD=BE£®ĄķÓÉČēĻĀ£ŗ£Ø1·Ö£©
”ß”÷ABCŗĶ”÷ADEĪŖµČ±ßČż½ĒŠĪ£¬
”ąAB=AC£¬AE=AD£¬”ĻBAC=”ĻEAD=60”ć£¬
”ß”ĻBAE=”ĻBAC-”ĻEAC=60”ć-”ĻEAC£¬
”ĻDAC=”ĻDAE-”ĻEAC=60”ć-”ĻEAC£¬
”ą”ĻBAE=”ĻDAC£¬£Ø3·Ö£©
”ą”÷DAC”Õ”÷EAB£ØSAS£©£¬
”ąCD=BE£®£Ø4·Ö£©
£Ø2£©”÷AMNŹĒµČ±ßČż½ĒŠĪ£®ĄķÓÉČēĻĀ£ŗ£Ø5·Ö£©
”ß”÷ABE”Õ”÷ACD£¬
”ą”ĻABE=”ĻACD
”ßM”¢N·Ö±šŹĒBE”¢CDµÄÖŠµć£¬
”ąBM=
BE=
CD=CN£¬
”ßAB=AC£¬”ĻABE=”ĻACD£¬
”ą”÷ABM”Õ”÷ACN£®
”ąAM=AN£¬”ĻMAB=”ĻNAC£®£Ø6·Ö£©
”ą”ĻNAM=”ĻNAC+”ĻCAM=”ĻMAB+”ĻCAM=”ĻBAC=60”ć£¬
”ą”÷AMNŹĒµČ±ßČż½ĒŠĪ£®£Ø7·Ö£©
ÉčAD=a£¬ŌņAB=2a£®
”ßAD=AE=DE£¬AB=AC£¬
”ąCE=DE£®
”ß”÷ADEĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻDEC=120”ć£¬”ĻADE=60”ć£¬
”ą”ĻEDC=”ĻECD=30”ć£¬
”ą”ĻADC=90”ć£®£Ø8·Ö£©
”ąŌŚRt”÷ADCÖŠ£¬AD=a£¬”ĻACD=30”ć£¬
”ąCD=
a£®
”ßNĪŖDCÖŠµć£¬
”ąDN=
a£¬
”ąAN=
==a£®£Ø9·Ö£©
”ß”÷ADE£¬”÷ABC£¬”÷AMNĪŖµČ±ßČż½ĒŠĪ£¬
”ąS
”÷ADE£ŗS
”÷ABC£ŗS
”÷AMN=a
2£ŗ£Ø2a£©
2£ŗ£Ø
a£©
2=1£ŗ4£ŗ
=4£ŗ16£ŗ7£Ø10·Ö£©
½ā·Ø¶ž£ŗ”÷AMNŹĒµČ±ßČż½ĒŠĪ£®ĄķÓÉČēĻĀ£ŗ£Ø5·Ö£©
”ß”÷ABE”Õ”÷ACD£¬M”¢N·Ö±šŹĒBE”¢CDµÄÖŠµć£¬
”ąAM=AN£¬NC=MB£®
”ßAB=AC£¬
”ą”÷ABM”Õ”÷ACN£¬
”ą”ĻMAB=”ĻNAC£¬
”ą”ĻNAM=”ĻNAC+”ĻCAM=”ĻMAB+”ĻCAM=”ĻBAC=60”ć£¬
”ą”÷AMNŹĒµČ±ßČż½ĒŠĪ£¬£Ø7·Ö£©
ÉčAD=a£¬ŌņAD=AE=DE=a£¬AB=BC=AC=2a£¬
Ņ×Ö¤BE”ĶAC£¬
”ąBE=
==a£¬
”ąEM=
a£¬
”ąAM=
==a£¬
”ß”÷ADE£¬”÷ABC£¬”÷AMNĪŖµČ±ßČż½ĒŠĪ£¬
”ąS
”÷ADE£ŗS
”÷ABC£ŗS
”÷AMN=a
2£ŗ£Ø2a£©
2£ŗ£Ø
a£©
2=1£ŗ4£ŗ
=4£ŗ16£ŗ7£®£Ø10·Ö£©






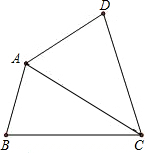 ĄūÓĆČż½ĒŠĪÄŚ½ĒŗĶ£¬Ģ½¾æĖıߊĪÄŚ½ĒŗĶ£ŗ
ĄūÓĆČż½ĒŠĪÄŚ½ĒŗĶ£¬Ģ½¾æĖıߊĪÄŚ½ĒŗĶ£ŗ