
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ������ڡ�ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ����������BCD���ƣ���ֱ��д�����е�P�����ֱ꣨��д�����������д�����̣���
���𰸡�
��1��
�⣺�ѵ�A��3��1������C��0��4��������κ���y=��x2+bx+c�ã�
![]() ���
��� ![]()
����κ�������ʽΪy=��x2+2x+4��
�䷽��y=����x��1��2+5��
���M��������1��5����
��2��
�⣺��ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4������ã�
![]() ���
��� ![]()
��ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F
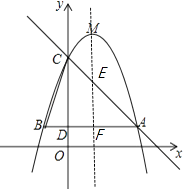
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1��
��1��5��m��3�����2��m��4��
��3��
�⣺����MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5��
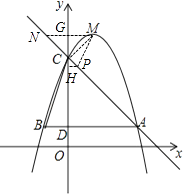
��MG=1��GC=5��4=1
��MC= ![]() =
= ![]() =
= ![]() ��
��
��y=5����y=��x+4���x=��1�����N��������1��5����
��NG=GC��GM=GC��
���NCG=��GCM=45�㣬
���NCM=90�㣬
�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ��
�����С�PCM�ס�BDC������ ![]()
��BD=1��CD=3��
��CP= ![]() =
= ![]() =
= ![]() ��
��
��CD=DA=3��
���DCA=45�㣬
����P��y���Ҳ࣬��PH��y�ᣬ
�ߡ�PCH=45�㣬CP= ![]()
��PH= ![]() =
= ![]()
��x= ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]() ��
��
��P1�� ![]() ����
����
ͬ���ɵã�����P��y����࣬���x=�� ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]()
��P2�� ![]() ,
, ![]() ����
����
�����С�PCM�ס�CDB������ ![]()
��CP= ![]() =3
=3 ![]()
��PH=3 ![]() ��
�� ![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7����
�����з�������õ�P������4�����ֱ�ΪP1�� ![]() ����P2��
����P2�� ![]() ,
, ![]() ��P3��3��1����P4����3��7����
��P3��3��1����P4����3��7����
�����������⿼���˶��κ�����ͼ�������ʡ�һ�κ�������ʽ���������������ʣ�����Ĺؼ��Ƿ����������������ƵIJ�ͬ������������ǵ�ʹ���������P�����꣮��1������A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ��2����M�����ŶԳ���ֱ��x=1����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=1���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ����3������������ɵá�MCP=90�㣬������PCM���BCD���ƣ���Ҫ���з������ۣ��ֳɡ�PCM�ס�BDC���PCM�ס�CDB���֣�Ȼ�����ñߵĶ�Ӧ��ֵ��������꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��С�����飬ÿһ�����Ϸֱ�д������1��2��3��4��5��6���������˷ֱ�Ӳ�ͬ�Ƕȹ۲�Ľ����ͼ��ʾ�������С��������Ե��������ϵ����ֱַ��Ƕ��٣�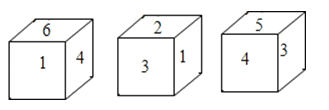
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�СΪ4��4�������������У������������ε��ǣ������� 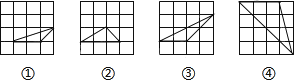
A.�ٺ͢�
B.�ں͢�
C.�ٺ͢�
D.�ں͢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ԥ������,ijѧУ�Խ��Ҳ���ҩ��������������,��֪ҩ��ȼ��ʱ,����ÿ���������еĺ�ҩ��y�����ˣ���ʱ��x�����ӣ���������,ҩ��ȼ�պ�,y��x�ɷ���������ͼ��,�ֲ�ҩ��8����ȼ��,��ʱ������ÿ������ҩ��Ϊ6����,������������ṩ����Ϣ,�ش���������
��1��ҩ��ȼ��ʱ,y����x�ĺ�����ϵʽΪ,�Ա���x��ȡֵ��Χ��;ҩ��ȼ�����,y��x�ĺ�����ϵʽΪ��
��2���о�����,�������е�ÿ�����ĺ�ҩ������1.6����ʱѧ�����ɽ�����,��ô��������ʼ,������Ҫ���������Ӻ�,ѧ�����ܻص����ң�
��3���о�����,��������ÿ�����ĺ�ҩ��������3�����ҳ���ʱ�䲻����10����ʱ,������Ч��ɱ������еIJ���,��ô�˴������Ƿ���Ч��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬BC=6��AC=8���ֱ��Ե�A��BΪԲ�ģ������߶�AB����һ��ij�Ϊ�뾶�������ཻ�ڵ�E��F������E��F��ֱ��EF����AB�ڵ�D������CD����CD�ij��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y= ![]() ��k��0����ͼ��A��B���㣬����A��AC��x�ᣬ����ΪC������B��BD��x�ᣬ����ΪD������AO������BO��AC�ڵ�E����OC=CD���ı���BDCE�����Ϊ2����k��ֵΪ ��
��k��0����ͼ��A��B���㣬����A��AC��x�ᣬ����ΪC������B��BD��x�ᣬ����ΪD������AO������BO��AC�ڵ�E����OC=CD���ı���BDCE�����Ϊ2����k��ֵΪ �� 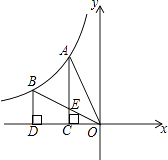
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���Գ���Ϊֱ��x= ![]() �������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA
�������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA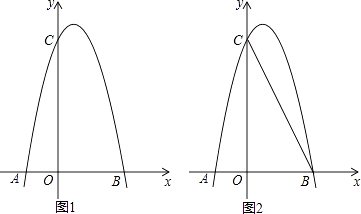
��1���������ߵĽ���ʽ��
��2������PΪ��һ�������������ϵ�һ�㣬���ı���COBP�����ΪS����S�����ֵ��
��3����ͼ2����M���߶�BC��һ���㣬��x���Ƿ���������ĵ�Q��ʹ��MQCΪ�����������ҡ�MQBΪֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������Ϊ��0��1������B��x���������ϵ�һ���㣬��ABΪ��������ֱ�ǡ�ABC��ʹ��BAC=90�㣬���B�ĺ�����Ϊx����C��������Ϊy���ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ� ��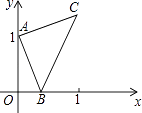
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ������֤��
��1���ⷽ���飺 ![]() ��
��
��2����ͼ��Rt��ABC�У���ACB=90�㣬��Rt��ABC���·��ۣ�ʹ��A���C�غϣ��ۺ�ΪDE����֤��DE��BC��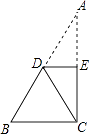
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com