
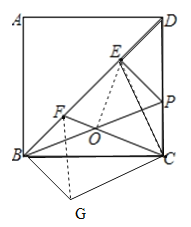
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.

(1) 如图1,求 ![]() 的值;
的值;
(2)O为BP的中点,连接CO并延长交BD于点F.
① 如图2,连接OE,求证:OE⊥OC;
② 如图3,若![]() ,求DP的长.
,求DP的长.
【答案】(1)![]() ;(2)①见解析;②4.
;(2)①见解析;②4.
【解析】试题分析:(1)由正方形的性质和PE⊥BD得到DP=![]() EP,即EP=
EP,即EP=![]() DP,代入原式即可得到结论;
DP,代入原式即可得到结论;
(2)①首先得出∠POE=2∠DBP,∠POC=2∠CBP,从而得到∠COE=∠POE+∠POC=2(∠DBP+∠CBP)=90°,即可得到结论;
② 连接OE、CE,把△DEC绕点C逆时针旋转90°得到△BGC,连结FG,则△BGC≌△DEC,得到EC=GC,DE=BG,∠GCB=∠ECD,∠GBC=∠EDC=45°,进而得到∠GCF=∠ECF.再证△GCF≌△ECF,得到EF=FG,在Rt△FBG中,有![]() ,即
,即![]() ,由已知
,由已知![]() ,设BF=3x,EF=5x,则DE=4x,得到3x+4x+5x=
,设BF=3x,EF=5x,则DE=4x,得到3x+4x+5x=![]() ,解得x的值,进而得到结论.
,解得x的值,进而得到结论.
试题解析:解:(1)∵ABCD是正方形,∴DC=AB=6,∠BDC=45°,∵PE⊥BD,∴△EPD是等腰直角三角形,∴DP=![]() EP,∴EP=
EP,∴EP=![]() DP,∴EP+
DP,∴EP+![]() CP=
CP=![]() DP +
DP +![]() CP=
CP=![]() (DP+CP)=
(DP+CP)=![]() DC=
DC=![]() ×6 =
×6 =![]() .
.
(2) ① ∵∠PEB=∠PCB=90°,O为BP的中点,∴OE=OB=OP=OC ,∴∠POE=2∠DBP,∠POC2∠CBP,∴∠COE=∠POE+∠POC=2(∠DBP+∠CBP)=90°,∴OE⊥OC;
② 连接OE、CE,把△DEC绕点C逆时针旋转90°得到△BGC,连结FG,则△BGC≌△DEC,∴EC=GC,DE=BG,∠GCB=∠ECD,∠GBC=∠EDC=45°.∵∠ECF=45°,∠BCD=90°,∴∠ECD+∠BFC=45°,∴∠GCF=45°,∴∠GCF=∠ECF.在△GCF和△ECF中,∵GC=EC,∠GCF=∠ECF,FC=FC,∴△GCF≌△ECF,∴EF=FG.∵∠DBC=∠GBC=45°,∴∠FBG=90°,∴![]() ,即
,即![]() ,∵
,∵![]() ,设BF=3x,EF=5x,则DE=4x,∴3x+4x+5x=
,设BF=3x,EF=5x,则DE=4x,∴3x+4x+5x=![]() ,解得x=
,解得x=![]() ,∴DP=
,∴DP=![]() DE=
DE=![]() x
x![]() .
.


科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若![]() , 求m和n的值
, 求m和n的值
解:∵![]()
∴![]()
∴![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
问题:(1)若![]() ,求
,求![]() 的值.
的值.
(2)已知a,b,c是△ABC的三边长,满足![]() ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:km/h).

(1)计算这些车的平均速度.
(2)车速的众数是多少?
(3)车速的中位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程 ![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围。
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
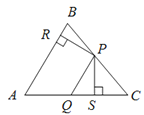
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若AQ
AB,若AQ![]() PQ,PR
PQ,PR![]() PS,则下列结论:①AS
PS,则下列结论:①AS![]() AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=![]() .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com