
【题目】如图,等边△ABC的边长为2,CD为AB边上的中线,E为线段CD上的动点,以BE为边,在BE左侧作等边△BEF,连接DF,则DF的最小值为_____.

【答案】![]()
【解析】
连接AF,由等边三角形的性质可证△ABF≌△CBE,可得∠BAF=∠BCE=30°,即当DF⊥AF时,DF的值最小,由直角三角形的性质可求DF的最小值.
解:如图,连接AF,

∵△ABC是等边三角形,CD为AB边上的中线,
∴AB=BC=2,AD=BD=1,∠ABC=∠ACB=60°,∠BCE=30°,
∵△BEF是等边三角形
∴BF=BE,∠FBE=60°
∴∠FBE=∠ABC,
∴∠ABF=∠CBE,且AB=BC,BF=BE,
∴△ABF≌△CBE(SAS)
∴∠BAF=∠BCE=30°,
∴当DF⊥AF时,DF的值最小,
此时,∠AFD=90°,∠FAB=30°,
∴AD=2DF
∴DF的最小值为![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
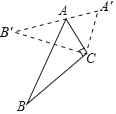
A. 65°B. 60°C. 50°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进中原经济区建设,促进中部地区崛起,我省汽车领头企业郑州日产实行技术革新,在保证原有生产线的同时,引进新的生产线,今年某月公司接到装配汽车2400辆的订单,定价为每辆6万元,若只采用新的生产线生产,则与原生产线相比可以提前8天完成订单任务,已知新的生产线使汽车装配效率比以前提高了![]() .
.
(1)求原生产线每天可以装配多少辆汽车?
(2)已知原生产线装配一辆汽车需要成本5万元,新生产线比原生产线每辆节省1万元,于是公司决定两条生产线同时生产,且新生产线装配的数量最多是原生产线装配数量的2倍,问:如何分配两条生产线才能使获得的利润最大,最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .证明:
.证明:![]() .
.
(2)如图(2),将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否仍然成立?如成立;请你给出证明;若不成立,请说明理由.
是否仍然成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点
上的两动点![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.
(1)第一批脐橙每件进价多少元?
(2)陈老板以每件120元的价格销售第二批脐橙,售出60%后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.

(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com