
【题目】如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.
(1)数轴上点A表示的数为 .点B表示的数为 ;
(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由;
(3)点P以每秒1个单位长度的速度从C点向左运动,点Q以每秒2个单位长度从点B出发向左运动,点R从点A以每秒5个单位长度的速度向右运动,它们同时出发,运动的时间为t秒,请求点P与点Q,点R的距离相等时t的值.

【答案】(1)-10;2 (2)存在;﹣12或4 (3)![]() 或4
或4
【解析】
(1)结合数轴可知点A和点B都在点C的左边,且点A小于0,在根据题意列式计算即可得到答案;
(2)因为AB=12,则P不可能在线段AB上,所以分两种情况:
①当点P在BA的延长线上时,②当点P在AB的延长线上时,进行讨论,即可得到答案;
(3)根据题意“t秒P点到点Q,点R的距离相等”,则此时点P、Q、R所表示的数分别是6﹣t,2﹣2t,﹣10+5t,分①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t)两种情况,计算即可得到答案.
解:(1)由题意可知点A和点B都在点C的左边,且点A小于0,则由题意可得数轴上点B表示的数为6-4=2,点A表示的数为2-10=﹣10,故答案为:﹣10,2;
(2)∵AB=12,
∴P不可能在线段AB上,
所以分两种情况:
①如图1,当点P在BA的延长线上时,PA+PB=16,

∴PA+PA+AB=16,
2PA=16﹣12=4,
PA=2,
则点P表示的数为﹣12;
②如图2,当点P在AB的延长线上时,同理得PB=2,

则点P表示的数为4;
综上,点P表示的数为﹣12或4;
(3)由题意得:t秒P点到点Q,点R的距离相等,则此时点P、Q、R所表示的数分别是6﹣t,2﹣2t,﹣10+5t,
①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),解得t=![]() ;
;
②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t),解得t=4;
答:点P与点Q,点R的距离相等时t的值是![]() 或4秒.
或4秒.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
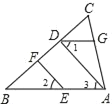
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)
解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B. 为了了解全国中学生的心理健康状况,应采用普查的方式
C. 一组数据0,1,2,1,1的众数和中位数都是1
D. 若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
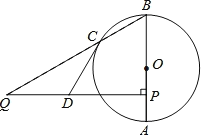
(1)点D在线段PQ上,且DQ=DC.求证:CD是⊙O的切线;
(2)若sin∠Q=![]() ,BP=6,AP=2,求QC的长.
,BP=6,AP=2,求QC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济的高速发展,有着“经济晴雨表”之称的股市也得到迅速的发展,下表是今年上证指数某一周星期一至星期五的变化情况.(注:上周五收盘时上证指数为2019点,每一天收盘时指数与前一天相比,涨记为“![]() ”,跌记为“
”,跌记为“![]() ”
” ![]()
星期 | 一 | 二 | 三 | 四 | 五 |
指数的变化(与前一天比较) |
|
|
|
|
|
(1)本周星期二收盘时的上证指数是 点;
(2)本周星期五收盘时的上证指数与上周星期五收盘时的上证指数相比,是增加了还是减少了?
(3)本周哪一天收盘时的上证指数最高?哪一天收盘时的上证指数最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每一个小正方形的边长为1.△ABC的三个顶点都在格点上,A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC向右平移6个单位的△A1B1C1,并写出C1的坐标 ;
(3)请画出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点。
![]()
(1)用1个单位长度表示1cm,请你在数轴上表示出A. B. C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm.
(3)若点B以每秒2cm的速度向左移动,同时A. C点分别以每秒1cm、4cm的速度向右移动。设移动时间为t秒,试探索:CAAB的值是否会随着t的变化而改变?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校组织的初中数学应用能力竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将八年级的一班和二班的成绩整理并绘制成如下的统计图,二班D级共有4人.

请你根据以上提供的信息解答下列问题:
(1)求此竞赛中一班共有多少人参加比赛,并补全条形统计图.
(2)扇形统计图中A级对应的圆心角度数是 .
(3)此次竞赛中二班在C级以上(包括C级)的人数为 .
(4)请你将表格补充完成:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com