

分析 (1)令x=0,求得A(0,2),令y=0,求得B(-3,0),C(1,0),由y=-$\frac{2}{3}$x2-$\frac{4}{3}$x+2转化成顶点式可知D(-1,$\frac{8}{3}$);
(2)①设P(n,0),则E(n,-$\frac{2}{3}$n2-$\frac{4}{3}$n+2),根据已知条件得出-$\frac{2}{3}$n2-$\frac{4}{3}$n+2=1-n,解方程即可求得E的坐标;
②根据直线ED和EA的斜率可知直线与坐标轴的交角相等,从而求得与坐标轴构成的三角形是等腰三角形,根据等腰三角形的性质即可求得EF的长;
③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,此时△PQR的周长PQ+QR+PR=EF,然后求得E、F的坐标,根据勾股定理即可求得.
解答 解:(1)令x=0,则y=2,
∴A(0,2),
令y=0,则-$\frac{2}{3}$x2-$\frac{4}{3}$x+2=0,解得x1=-3,x2=1(舍去),
∴B(-3,0),C(1,0),
由y=-$\frac{2}{3}$x2-$\frac{4}{3}$x+2=-$\frac{2}{3}$(x+1)2+$\frac{8}{3}$可知D(-1,$\frac{8}{3}$),
故答案为:0、2,-3、0,1、0,-1、$\frac{8}{3}$;
(2)①设P(n,0),则E(n,-$\frac{2}{3}$n2-$\frac{4}{3}$n+2),
∵PE=PC,
∴-$\frac{2}{3}$n2-$\frac{4}{3}$n+2=1-n,解得n1=-$\frac{3}{2}$,n2=1(舍去),
∴当n=-$\frac{3}{2}$时,1-n=$\frac{5}{2}$,
∴E(-$\frac{3}{2}$,$\frac{5}{2}$),
②如图1,设直线DE与x轴交于M,与y轴交于N,直线EA与x轴交于K,
根据E、D的坐标求得直线ED的斜率为$\frac{1}{3}$,根据E、A的坐标求得直线EA的斜率为-$\frac{1}{3}$,
∴△MEK是以MK为底边的等腰三角形,△AEN是以AN为底边的等腰三角形,
∵到EA和ED的距离相等的点F在顶角的平分线上,
根据等腰三角形的性质可知,EF是E点到坐标轴的距离,
∴EF=$\frac{3}{2}$或$\frac{5}{2}$;
(3)根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,
如图2,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,
此时△PQR的周长PQ+QR+PR=EF,
∵A(0,2),B(-3,0),C(1,0),
∴AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵S△AOB=$\frac{1}{2}$×$\frac{1}{2}$OE×AB=$\frac{1}{2}$OA•OB,
∴OE=$\frac{12}{\sqrt{13}}$,
∵△OEM∽△ABO,
∴$\frac{OM}{OA}$=$\frac{EM}{OB}$=$\frac{OE}{AB}$,即$\frac{OM}{2}$=$\frac{EM}{3}$=$\frac{\frac{12}{\sqrt{13}}}{\sqrt{13}}$,
∴OM=$\frac{24}{13}$,EM=$\frac{36}{13}$
∴E(-$\frac{24}{13}$,$\frac{36}{13}$),
同理求得F($\frac{8}{5}$,$\frac{4}{5}$),
即△PQR周长的最小值为EF=$\sqrt{(\frac{8}{5}+\frac{24}{13})^{2}+(\frac{36}{13}-\frac{4}{5})^{2}}$=$\frac{32\sqrt{65}}{65}$.
点评 本题是二次函数的综合题,考查了二次函数的性质,角平分线的性质,等腰三角形的性质,勾股定理的应用,轴对称-最短路线问题,(3)根据对称的性质确定出三角形周长最小时满足的图形,找出点P关于直线AB的对称点E,关于AC的对称点F,再根据两点之间线段最短得到BEF即为PQ+QR+PR的最小值是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | 2015 | D. | -2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -3 | C. | 4 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
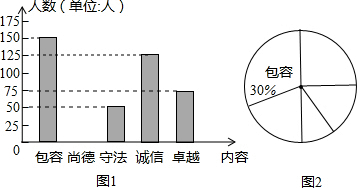
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.
如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
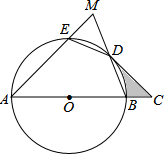 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款的数额(单位:元) | 20 | 50 | 80 | 100 |
| 人数(单位:名) | 6 | 7 | 4 | 3 |
| A. | 20元 | B. | 50元 | C. | 80元 | D. | 100元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com