
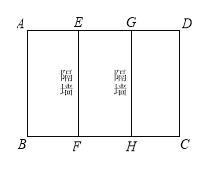
����Ŀ����ͼ��ʾ����ˮ������˾Ϊij¥����һ���ܳ�Ϊ30��������ˮ�����أ�ƽ��ͼΪ����![]() ��
��![]() �ף��м�������ǽ�ֱ�Ϊ
�ף��м�������ǽ�ֱ�Ϊ![]() ��
��![]() ����ǽ�ĺ�Ȳ����ǣ�
����ǽ�ĺ�Ȳ����ǣ�
(1)�ú�![]() �Ĵ���ʽ��ʾ��Χǽ
�Ĵ���ʽ��ʾ��Χǽ![]() �ij��ȣ�
�ij��ȣ�
(2)������ʱҪ�����ˮ��![]() ǡ�ñ���ǽ�ֳ�����ȫ�ȵľ��Σ������Ǿ������
ǡ�ñ���ǽ�ֳ�����ȫ�ȵľ��Σ������Ǿ������![]() ���ƣ����ʱ
���ƣ����ʱ![]() �ij���
�ij���
(3)������ʱҪ�����ˮ��![]() ǡ�ñ���ǽ�ֳ�����ȫ�ȵ�������.��֪�ص���Χǽ���쵥��Ϊÿ��400Ԫ���м�������ǽ���쵥��ÿ��300Ԫ���ص���ĵ���Ϊÿƽ����100Ԫ.�Լ������̵������.�������ȷ��1Ԫ��
ǡ�ñ���ǽ�ֳ�����ȫ�ȵ�������.��֪�ص���Χǽ���쵥��Ϊÿ��400Ԫ���м�������ǽ���쵥��ÿ��300Ԫ���ص���ĵ���Ϊÿƽ����100Ԫ.�Լ������̵������.�������ȷ��1Ԫ��
���𰸡���1��AD=15-x����2��![]() ����3��18469.
����3��18469.
��������
������1�����ݾ��ε��ܳ������������ߺ͵�2��������AD=15-x(��)��
��2������������֪![]() ����
����![]() ����
����![]() ���ݴ˿��з���
���ݴ˿��з���![]() �����AB�ij���
�����AB�ij���
��3�����������֪AD=3x�ף�����15-x=3x�����x��ֵ������������.
�����������1��![]() �ף�
�ף�
��2���������֪��![]() ����
����![]() ����
����![]()
��![]()
��ã�![]() ��
��![]() (�������⣬��ȥ)
(�������⣬��ȥ)
��![]()
��3��������֪![]() �ף�����
�ף�����![]()
���![]()
����ۣ�![]() =
=![]()
��![]() ʱ��ԭʽ=
ʱ��ԭʽ=![]()
![]() (Ԫ)
(Ԫ)
�𣺴���̵������ԼΪ18469Ԫ.
����: ��1��һԪ�������̵�Ӧ�ã���2��һԪһ�η��̵�Ӧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�͡�DBE���Ƶ�B��ת���������������Σ����С�ABC���DBE����A���DΪ��Ӧ�ǣ�
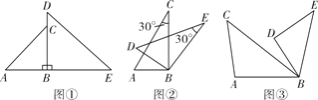
(1)��ͼ�٣�����ABC�͡�DBE�ֱ����ԡ�ABC���DBEΪ���ǵĵ���ֱ�������Σ�������������ת��ʹ��B��C��D��ͬһ��ֱ���ϵ�λ��ʱ����ֱ��д���߶�AD���߶�EC�Ĺ�ϵ��
(2)����ABC�͡�DBEΪ����30��ǵ�ֱ�������Σ���������������ת����ͼ�ڵ�λ��ʱ����ȷ���߶�AD���߶�EC�Ĺ�ϵ����˵�����ɣ�
(3)����ABC�͡�DBEΪ��ͼ�۵����������Σ��ҡ�ACB��������BDE���������Ƶ�B��ת�Ĺ����У�ֱ��AD��EC�нǵĶ����Ƿ�ı䣿�����ı䣬ֱ���ú���������ʽ�ӱ�ʾ�нǵĶ��������ı䣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
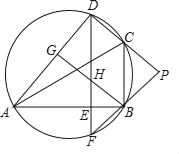
����Ŀ����ͼ��D����ABC���Բ�ϵĵ㣬��B��Dλ��AC�����࣬DE��AB������ΪE��DE���ӳ��߽���Բ�ڵ�F��BG��AD������ΪG��BG��DE�ڵ�H��DC��FB���ӳ��߽��ڵ�P����PC=PB��
��1����֤����BAD=��PCB��
��2����֤��BG��CD��
��3������ABC���Բ��Բ��ΪO����AB=![]() DH����COD=23�������P�Ķ�����
DH����COD=23�������P�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=2x�ͷ�����������ͼ���ڵ�A��m����2����

��1�����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д������������ֵ���ڷ���������ֵʱ�Ա���x��ȡֵ��Χ��
��3����˫�����ϵ�C��2��n����OA����ƽ��![]() ����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ��,��C,D����O��,��AB��5,BC��3.
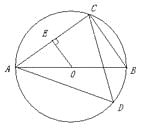
(1) ��sin��BAC��ֵ;
(2) ���OE��AC, ����ΪE,��OE�ij�;
(3) ��tan��ADC��ֵ.(�����������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
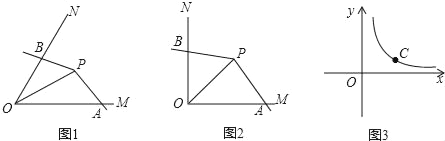
����Ŀ����ͼ1����PΪ��MON��ƽ������һ�㣬��PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�����APB�Ƶ�P��תʱʼ������OAOB��OP2�����ǾͰѡ�APB������MON���ǻ۽ǣ�
��1����ͼ2����֪��MON��90�㣬��PΪ��MON��ƽ������һ�㣬��PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�ҡ�APB��135�㣮��֤����APB�ǡ�MON���ǻ۽ǣ�
��2����ͼ1����֪��MON������0�㣼����90�㣩��OP��2������APB�ǡ�MON���ǻ۽ǣ�����AB���ú�����ʽ�ӷֱ��ʾ��APB�Ķ����͡�AOB�������
��3����ͼ3��C�Ǻ���y��![]() ��x��0��ͼ���ϵ�һ�����㣬��C��ֱ��CD�ֱ�x���y����A��B���㣬������BC��2CA���������AOB���ǻ۽ǡ�APB�Ķ���P�����꣮
��x��0��ͼ���ϵ�һ�����㣬��C��ֱ��CD�ֱ�x���y����A��B���㣬������BC��2CA���������AOB���ǻ۽ǡ�APB�Ķ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c(a��0)��ͼ����ͼ��ʾ��������4�����ۣ���abc��0����b��a+c����4a+2b+c��0����b2-4ac��0��������ȷ�Ľ�����________(�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABΪ��ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��ֱ��AB�ij�Ϊ4����BC=2����DAC=15�㣮
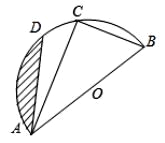
(1)����DAB�Ķ�����
(2)��ͼ����Ӱ���ֵ����(���������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
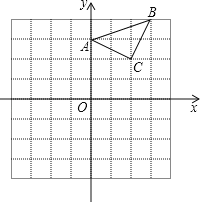
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
��1��������ABC����ƽ��4����λ���ȵõ�����A1B1C1����C1���������� ��
��2���Ե�BΪλ�����ģ��������ڻ�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2���������� ����
��3����A2B2C2��������� ��ƽ����λ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com