
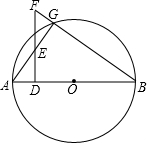
 如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.
如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.科目:初中数学 来源: 题型:
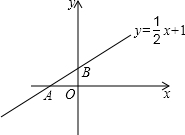 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
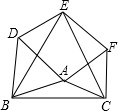 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形:△ABD,△BCE,△ACF,请解答下列问题:
如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形:△ABD,△BCE,△ACF,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| 班别 | (1)班 | (2)班 | (3)班 | (4)班 |
| 捐款人数 | 37 | 36 | 47 | |
| 捐款金额(元) | 183 | 162 | 175 | 280 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
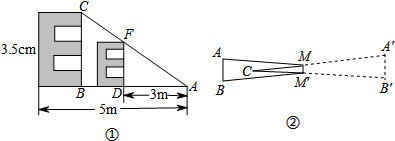
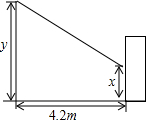 我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上.
我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上.查看答案和解析>>
科目:初中数学 来源: 题型:
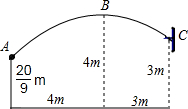 如图,一场篮球赛中,球员甲跳起投篮,已知球出手时离地面
如图,一场篮球赛中,球员甲跳起投篮,已知球出手时离地面| 20 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com