

 =
=
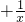 ,
, ,.
,. ,救生圈沿着航行方向漂流全程的
,救生圈沿着航行方向漂流全程的 ,船与救生圈同向而行,距离拉大,船到B港后立刻掉头去找救生圈,1小时后找到,在这一小时内,船与救生圈相向而行,将原已拉开的距离缩短为0,
,船与救生圈同向而行,距离拉大,船到B港后立刻掉头去找救生圈,1小时后找到,在这一小时内,船与救生圈相向而行,将原已拉开的距离缩短为0, -
- )=1×(
)=1×(
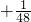 ),
), ,根据小船早晨6时从港出发,顺流航行需6小时,得出它在中午12点钟到达B港,根据救生圈在y点钟就已掉下水,到这时已漂流的时间为(12-y)小时,在这段时间里,每小时船行驶全程的
,根据小船早晨6时从港出发,顺流航行需6小时,得出它在中午12点钟到达B港,根据救生圈在y点钟就已掉下水,到这时已漂流的时间为(12-y)小时,在这段时间里,每小时船行驶全程的 ,救生圈沿着航行方向漂流全程的
,救生圈沿着航行方向漂流全程的 ,船与救生圈同向而行,距离拉大,船到B港后立刻掉头去找救圈,1小时后找到,在这一小时内,船与救生圈相向而行,将原已拉开的距离缩短为0,列出方程,求出方程的解即可.
,船与救生圈同向而行,距离拉大,船到B港后立刻掉头去找救圈,1小时后找到,在这一小时内,船与救生圈相向而行,将原已拉开的距离缩短为0,列出方程,求出方程的解即可.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com