
【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

【答案】(1)40,20;(2) 20;(3)详见解析
【解析】
(1)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,即可求出答案;
(2)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,即可求出答案;
(3)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,最后代入求出即可.
解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°-(∠B+∠C)=80°,
∵AE是角平分线,
∴∠CAE=![]() =40°,
=40°,
∵AD是高,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-∠ADC-∠C=20°,
∴∠DAE=∠CAE-∠CAD=40°-20°=20°,
故答案为:40,20;
(2)∵∠B=40°,∠C=80°,
∴∠BAC=180°-(∠B+∠C)=60°,
∵AE是角平分线,
∴∠CAE=![]() =30°,
=30°,
∵AD是高,
∴∠ADC=90°,
∵∠C=80°,
∴∠DAC=180°-∠ADC-∠C=10°,
∴∠DAE=∠CAE-∠CAD=30°-10°=20°,
故答案为:20;
(3)∵∠BAC +∠B+∠C=180°,
∴∠BAC=180°-(∠B+∠C),
∵AE是角平分线,
∴∠CAE=![]()
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∴∠DAE=∠CAE-∠CAD
![]()
![]()
![]()
![]()
=20°.


科目:初中数学 来源: 题型:
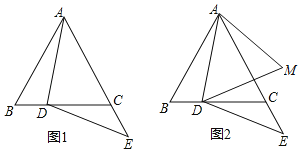
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元
B.4元
C.6元
D.8元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
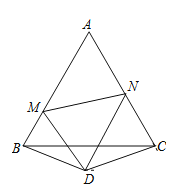
【题目】如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象与一次函数
的图象与一次函数 ![]() 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).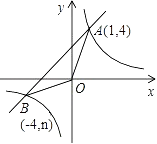
(1)求 ![]() 和
和 ![]() 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com