
【题目】如图1,长方形OABC的边OA、OC分别在x轴、y轴上,B点坐标是(8,4),将△AOC沿对角线AC翻折得△ADC,AD与BC相交于点E.
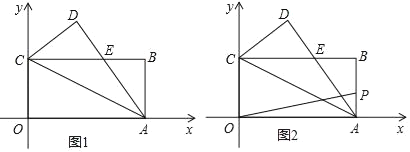
(1)求证:△CDE≌△ABE
(2)求E点坐标;
(3)如图2,动点P从点A出发,沿着折线A→B→C→O运动(到点O停止),是否存在点P,使得△POA的面积等于△ACE的面积,若存在,直接写出点P坐标,若不存在,说明理由.
【答案】(1)见解析;(2)E(5,4);(3)存在,满足条件的点P的坐标为(8,![]() )或(0,
)或(0,![]() ),理由见解析
),理由见解析
【解析】
(1)用角角边定理即可证明.
(2)设CE=AE=n,则BE=8-n,利用勾股定理即可求解.
(3)构建方程确定点P的纵坐标即可解决问题.
解:(1)证明:∵四边形OABC为矩形,
∴AB=OC,∠B=∠AOC=90°,
∴CD=OC=AB,∠D=∠AOC=∠B,
又∠CED=∠ABE,
∴△CDE≌△ABE(AAS),
∴CE=AE;
(2)∵B(8,4),即AB=4,BC=8.
∴设CE=AE=n,则BE=8﹣n,
可得(8﹣n)2+42=n2,
解得:n=5,
∴E(5,4);
(3)∵S△ACE=![]() CEAB=
CEAB=![]() ×5×4=10,
×5×4=10,
∴S△POA=![]() OAyP=10,
OAyP=10,
∴![]() ×8×yP=10,
×8×yP=10,
∴yP=![]() ,
,
∴满足条件的点P的坐标为(8,![]() )或(0,
)或(0,![]() ).
).


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中数学 来源: 题型:
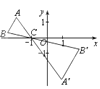
【题目】如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. -![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布条形图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断:
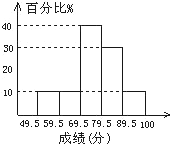
(1)成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等;
(2)成绩在79.5~89.5分段的人数占30%;
(3)成绩在79.5分以上的学生有20人;
(4)本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
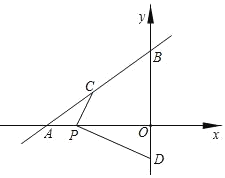
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com