
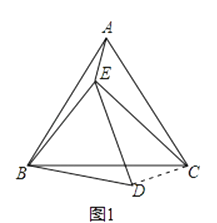
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°. 
(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= ![]() AE;
AE;
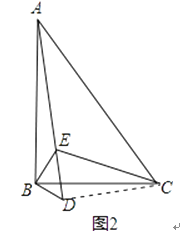
(2)当α=90°时(如图2),求 ![]() 的值.
的值.
【答案】
(1)解:①判断:△ABC是等边三角形.
理由:∵∠ABC=∠ACB=60°
∴∠BAC=180°﹣∠ABC﹣∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形
②证明:同理△EBD也是等边三角形
连接DC,
则AB=BC,BE=BD,∠ABE=60°﹣∠EBC=∠CBD
∴△ABE≌△CBD
∴AE=CD,∠AEB=∠CDB=150°
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣60°=30°
在Rt△EDC中 ![]() ,
,
∴ ![]()
(2)解:连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴ ![]()
又∵∠ABE=90°﹣∠EBC=∠CBD
∴△ABE∽△CBD,∠AEB=∠CDB=150°, ![]()
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣(90°﹣∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE= ![]()
在Rt△EDC中CD= ![]()
∴ ![]() ,即
,即 ![]()
【解析】①由三角形ABC中有两个60°而求得它为等边三角形;②由△EBD也是等边三角形,连接DC,证得△ABE≌△CBD,在直角三角形中很容易证得结论.(2)连接DC,证得△ABC∽△EBD,设BD=x在Rt△EBD中DE=2x由相似比即得到比值.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
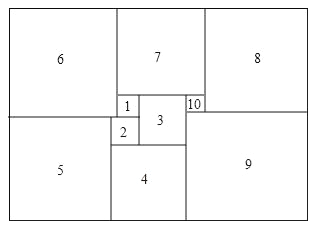
【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算:
(1)如果标注1、2的正方形边长分别为1,2,第3个正方形的边长= ;第5个正方形的边长= ;
(2)如果标注1、2的正方形边长分别为x,y,第10个正方形的边长= .(用含x、y的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,若购买1张两人学习桌,1张三人学习桌需230元;若购买2张两人学习桌,3张三人学习桌需590元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6600元,购买两种学习桌共60张,以至少满足137名学生的需求,有几种购买方案?并求哪种购买方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA=OB,∠A=∠B,有下列4个结论:①△AOD≌△BOC,②EA=EB,③点E在∠O的平分线上.④若OC=2CA,△AEC的面积为1,那么四边形OCED的面积为4.其中正确的结论个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12cm,且![]() ,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,△CPQ的周长为18cm,问:经过几秒后,△CPQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字. 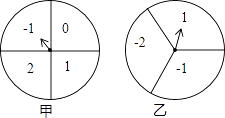
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小刚站在河边的A点处,在河对面(小刚的正北方向)的B处有一电视塔,小刚想知道电线塔离他有多远,于是他向正西走了20步到达一棵树C处,接着继续向前走了20步到达D处,然后他左转90°直行,当他看到的电线塔B,树C和自己所处的位置E在一条直线上时,他在整个步测过程中共走了100步.
(1)根据题意,画出示意图;
(2)如果小刚的一步大约有50cm长,请你估计小刚的初始位置A与电线塔B之间的距离,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=![]() (k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为
(k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为![]() ,点C的横坐标为1.
,点C的横坐标为1.
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com