
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
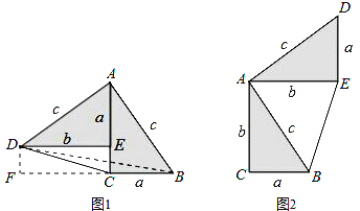
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连接 ,
∵S五边形ACBED= ,
又∵S五边形ACBED= ,
∴ ,
∴a2+b2=c2.
科目:初中数学 来源: 题型:
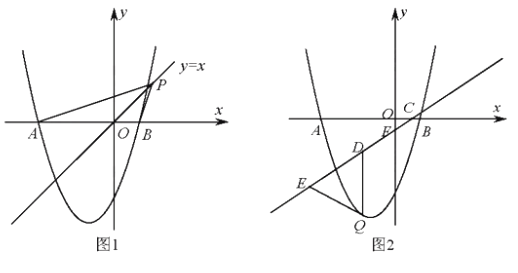
【题目】(2016广东省深圳市第23题)如图,抛物线![]() 与
与![]() 轴交于A、B两点,且B(1 , 0)。
轴交于A、B两点,且B(1 , 0)。
(1)、求抛物线的解析式和点A的坐标;
(2)、如图1,点P是直线![]() 上的动点,当直线
上的动点,当直线![]() 平分∠APB时,求点P的坐标;
平分∠APB时,求点P的坐标;
(3)如图2,已知直线![]() 分别与
分别与![]() 轴
轴 ![]() 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作
轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作 ![]() 轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬“中国梦”,某校初三(1)班和(2)班各5名学生参加以“诚信友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:
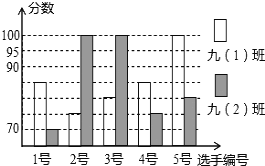
(1)求初三(1)班5名同学得分的平均数和初三(2)班5名同学得分的众数;
(2)你认为哪个班5名同学参赛的整体成绩要好些?为什么?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①DF=DN ②AE=CN;③△DMN是等腰三角形;④∠BMD=45°,其中正确的结论个数是 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | 0.12 | ﹣0.02 | ﹣0.13 | ﹣0.20 | ﹣0.08 | ﹣0.02 | 0.32 |
A. 星期二 B. 星期四 C. 星期六 D. 星期五
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com