
分析 (1)根据题意列出方程组求解即可;
(2)将两车的费用相加即可求得总费用的函数解析式;
(3)根据一次函数得到当x越小时,总费用越小,分别代入1,2,3,4得到最小值即可.
解答 解:(1)设甲种货车x辆,乙种货车y辆,
根据题意得:$\left\{\begin{array}{l}{x+3y=29}\\{2x+3y=37}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=7}\end{array}\right.$,
答:甲车装8吨,乙车装7吨;
(2)设甲车x辆,则乙车为(8-x)辆,
根据题意得:w=500x+450(8-x)=50x+3600(1≤x≤8);
(3)∵当x=1时,则8-x=7,w=8+7×7=57<60吨,不合题意;
当x=2时,则8-x=6,w=8×2+7×6=58<60吨,不合题意;
当x=3时,则8-x=5,w=8×3+7×5=59<60吨,不合题意;
当x=4时,则8-x=4,w=8×4+7×4=60吨,符合题意;
∴租用4辆甲车,4辆乙车时总运费最省,为50×4+3600=3800元.
点评 该题主要考查了列二元一次方程组或二元一次方程来解决现实生活中的实际应用问题;解题的关键是深入把握题意,准确找出命题中隐含的数量关系,正确列出方程或方程组来分析、推理、解答.


科目:初中数学 来源: 题型:解答题
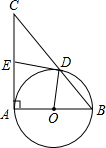 如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )| A. | 60° | B. | 120° | C. | 60°或120° | D. | 30°或150° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为27.8°(用科学计算器计算,结果精确到0.1°).
如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为27.8°(用科学计算器计算,结果精确到0.1°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com