
 已知,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
已知,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.分析 (1)根据平行四边形的性质可得到对应角相等对应边相等,从而不难求得其周长;
(2)根据中位线的性质及菱形的判定不难求得四边形AQMP为菱形.
解答 解:(1)∵AB∥MP,QM∥AC,
∴四边形APMQ是平行四边形,∠B=∠PMC,∠C=∠QMB.
∵AB=AC,
∴∠B=∠C,
∴∠PMC=∠QMB.
∴BQ=QM,PM=PC.
∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a;
(2)当点M在BC的中点时,四边形APMQ是菱形,
∵AB∥MP,点M是BC的中点,
∴$\frac{CM}{CB}$=$\frac{CP}{AC}$=$\frac{1}{2}$,
∴P是AC的中点,
∴PM是三角形ABC的中位线,
同理:QM是三角形ABC的中位线.
∵AB=AC,
∴QM=PM=$\frac{1}{2}$AB=$\frac{1}{2}$AC.
又由(1)知四边形APMQ是平行四边形,
∴平行四边形APMQ是菱形.
点评 此题主要考查了平行四边形的判定和性质,中位线的性质,菱形的判定等知识点的综合运用.


科目:初中数学 来源: 题型:选择题
 一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )| A. | 3π | B. | 18π | C. | 8π | D. | 9π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为( )
如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为( )| A. | 24° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形的两边长分别为3和4,则斜边长为5 | |
| B. | △ABC中∠A、∠B、∠C的对边分别是a、b、c,如果(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 菱形的对角线相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
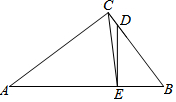 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D在边BC上,BD=5CD,DE⊥AB,垂足为E.
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D在边BC上,BD=5CD,DE⊥AB,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+y=4 | B. | 2x+y=4m | C. | 2x+y=-4 | D. | 2x+y=-4m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com