

·ÖĪö £Ø1£©øł¾ŻĖıߊĪABCDŹĒ”°µČ¶Ō½ĒĖıߊĪ”±µĆ³ö”ĻD=”ĻB=80”ć£¬øł¾Ż¶ą±ßŠĪÄŚ½ĒŗĶ¶ØĄķĒó³ö”ĻC¼“æÉ£»
£Ø2£©Į¬½ÓBD£¬ÓÉAB=AD£¬µĆ³ö”ĻABD=”ĻADB£¬Ö¤³ö”ĻCBD=”ĻCDB£¬¼“æÉµĆ³öCB=CD£»
£Ø3£©·ÖĮ½ÖÖĒéæö£ŗ¢Łµ±”ĻADC=”ĻABC=90”揱£¬ŃÓ³¤AD£¬BCĻą½»ÓŚµćE£¬ĻČÓƵČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹĒó³öAE£¬µĆ³öDE£¬ŌŁÓĆČż½ĒŗÆŹżĒó³öCD£¬Óɹ“¹É¶ØĄķĒó³öAC£»
¢Śµ±”ĻBCD=”ĻDAB=45”揱£¬¹żµćD×÷DM”ĶABÓŚµćM£¬DN”ĶBCÓŚµćN£¬Ōņ”ĻAMD=90”ć£¬ĖıߊĪBNDMŹĒ¾ŲŠĪ£¬ĻČĒó³öAM”¢DM£¬ŌŁÓɾŲŠĪµÄŠŌÖŹµĆ³öDN=BM=1£¬BN=DM=4£¬Ēó³öCN”¢BC£¬øł¾Ż¹“¹É¶ØĄķĒó³öAC¼“æÉ£®
½ā“š £Ø1£©½ā£ŗ”ßĖıߊĪABCDŹĒ”°µČ¶Ō½ĒĖıߊĪ”±£¬”ĻA”Ł”ĻC£¬
”ą”ĻD=”ĻB=80”ć£¬
”ą”ĻC=360”ć-”ĻA-”ĻB-”ĻD=360”ć-70”ć-80”ć-80”ć=130”ć£»
£Ø2£©Ö¤Ć÷£ŗČēĶ¼2ĖłŹ¾£¬Į¬½ÓBD£¬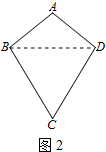
”ßAB=AD£¬
”ą”ĻABD=”ĻADB£¬
”ß”ĻABC=”ĻADC£¬
”ą”ĻABC-”ĻABD=”ĻADC-”ĻADB£¬
”ą”ĻCBD=”ĻCDB£¬
”ąCB=CD£»
£Ø3£©½ā£ŗ·ÖĮ½ÖÖĒéæö£ŗ
¢Łµ±”ĻADC=”ĻABC=90”揱£¬ŃÓ³¤AD£¬BCĻą½»ÓŚµćE£¬ČēĶ¼3ĖłŹ¾£ŗ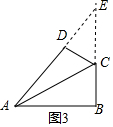
”ß”ĻABC=90”ć£¬”ĻDAB=45”ć£¬AB=5£¬”ą”ĻE=45”ć£¬
”ąAE=$\sqrt{2}$AB=5$\sqrt{2}$£¬
”ąDE=AE-AD=5$\sqrt{2}$-4$\sqrt{2}$ØT$\sqrt{2}$£¬
”ß”ĻEDC=90”ć£¬”ĻE=45”ć£¬
”ąCD=$\sqrt{2}$£¬
”ąAC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{£Ø\sqrt{2}£©^{2}+£Ø4\sqrt{2}£©^{2}}$=$\sqrt{34}$£»
¢Śµ±”ĻBCD=”ĻDAB=45”揱£¬
¹żµćD×÷DM”ĶABÓŚµćM£¬DN”ĶBCÓŚµćN£¬ČēĶ¼4ĖłŹ¾£ŗ
Ōņ”ĻAMD=90”ć£¬ĖıߊĪBNDMŹĒ¾ŲŠĪ£¬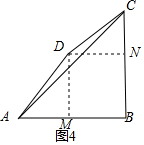
”ß”ĻDAB=45”ć£¬
”ą”ĻADM=45”ć£¬
”ąAM=DM=$\frac{\sqrt{2}}{2}$AD=4£¬
”ąBM=AB-AM=5-4=1£¬
”ßĖıߊĪBNDMŹĒ¾ŲŠĪ£¬
”ąDN=BM=1£¬BN=DM=4£¬
”ß”ĻBCD=45”ć£¬
”ąCN=DN=1£¬
”ąBC=CN+BN=5£¬
”ąAC=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$£»
¹Ź“ĖĒéæö²»“ęŌŚ£®
×ŪÉĻĖłŹö£ŗACµÄ³¤ĪŖ$\sqrt{34}$£¬
¹Ź“š°øĪŖ£ŗ$\sqrt{34}$£®
µćĘĄ ±¾ĢāŹĒĖıߊĪ×ŪŗĻĢāÄ棬漲éĮĖŠĀ¶ØŅ唢ĖıߊĪÄŚ½ĒŗĶ¶ØĄķ”¢µČŃüČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢¹“¹É¶ØĄķ”¢Čż½ĒŗÆŹż”¢¾ŲŠĪµÄÅŠ¶ØÓėŠŌÖŹµČÖŖŹ¶£»±¾ĢāÄŃ¶Č½Ļ“ó£¬×ŪŗĻŠŌĒ棬ĢŲ±šŹĒ£Ø3£©ÖŠ£¬ŠčŅŖ½ųŠŠ·ÖĄąĢÖĀŪ£¬Ķعż×÷øØÖśĻßŌĖÓĆČż½ĒŗÆŹżŗĶ¹“¹É¶ØĄķ²ÅÄÜµĆ³ö½į¹ū£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
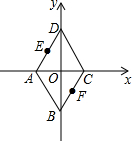 ŅŌĮāŠĪABCDµÄ¶Ō½ĒĻß½»µćOĪŖŌµć£¬¶Ō½ĒĻßAC”¢BDĖłŌŚÖ±ĻßĪŖ×ų±źÖį£¬½ØĮ¢ČēĶ¼ĖłŹ¾Ö±½Ē×ų±źĻµ£¬ADµÄÖŠµćEµÄ×ų±źĪŖ£Ø-1£¬2£©£¬ŌņBCµÄÖŠµćFµÄ×ų±źĪŖ£Ø1£¬-2£©£®
ŅŌĮāŠĪABCDµÄ¶Ō½ĒĻß½»µćOĪŖŌµć£¬¶Ō½ĒĻßAC”¢BDĖłŌŚÖ±ĻßĪŖ×ų±źÖį£¬½ØĮ¢ČēĶ¼ĖłŹ¾Ö±½Ē×ų±źĻµ£¬ADµÄÖŠµćEµÄ×ų±źĪŖ£Ø-1£¬2£©£¬ŌņBCµÄÖŠµćFµÄ×ų±źĪŖ£Ø1£¬-2£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
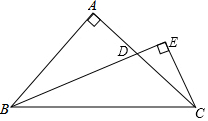 ŅŃÖŖµČŃüÖ±½ĒČż½ĒŠĪABC£¬BCŹĒŠ±±ß£¬”ĻBµÄĘ½·ÖĻß½»ACÓŚD£¬¹żC×÷CEÓėBD“¹Ö±ĒŅ½»BDŃÓ³¤ĻßÓŚE£®ŅŃÖŖCE=4£¬ŌņBDµÄ³¤ĪŖ£Ø””””£©
ŅŃÖŖµČŃüÖ±½ĒČż½ĒŠĪABC£¬BCŹĒŠ±±ß£¬”ĻBµÄĘ½·ÖĻß½»ACÓŚD£¬¹żC×÷CEÓėBD“¹Ö±ĒŅ½»BDŃÓ³¤ĻßÓŚE£®ŅŃÖŖCE=4£¬ŌņBDµÄ³¤ĪŖ£Ø””””£©| A£® | 5 | B£® | 8 | C£® | $\sqrt{73}$ | D£® | 7 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
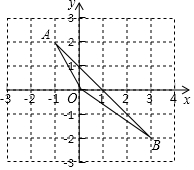 ŅŃÖŖ£ŗµćA”¢BŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬
ŅŃÖŖ£ŗµćA”¢BŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com