
分析 分两种情况:①根据平行四边形的性质AB=CD,AD=BC,由勾股定理求出BE和CE,得出BC,即可得出结果;②同①得:BC=BE-CE=1,得出?ABCD的周长=2(AB+BC)=12,即可得出结论.
解答  解:分两种情况:
解:分两种情况:
①如图所示:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AE⊥BC,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,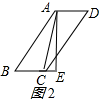
∴BC=BE+CE=5,
∴?ABCD的周长=2(AB+BC)=2×10=20;
②如图2所示:
同①得:BC=BE-CE=1,
∴?ABCD的周长=2(AB+BC)=2×6=12;
综上所述:?ABCD的周长为20或12;
故答案为:20或12.
点评 此题主要考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出BE和CE是解决问题的关键,注意分类讨论.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $2\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为喜迎G20,某校团委举办了以“G20”为主题的学生绘画展览,为美化画面,要在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),若设彩纸的宽度为xcm,根据题意可列方程为( )
为喜迎G20,某校团委举办了以“G20”为主题的学生绘画展览,为美化画面,要在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),若设彩纸的宽度为xcm,根据题意可列方程为( )| A. | (30+2x)(20+2x)=1200 | B. | (30+x)(20+x)=1200 | C. | (30-2x)(20-2x)=600 | D. | (30+x)(20+x)=600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,点E为BC上一点,AE为∠BAF的角平分线,∠FAD比∠FAE大48°,设∠FAE和∠FAD的度数分别为x,y,那么x,y所适合的一个方程组是( )
如图,正方形ABCD中,点E为BC上一点,AE为∠BAF的角平分线,∠FAD比∠FAE大48°,设∠FAE和∠FAD的度数分别为x,y,那么x,y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}{y-x=48°}\\{y=2x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=48°}\\{y+2x=90°}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-x=48°}\\{y+x=90°}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=48°}\\{2x+y=90°}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com