
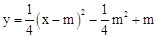 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.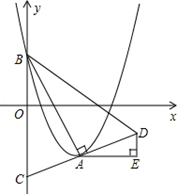
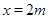 ,
,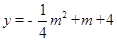 ,将
,将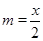 代入
代入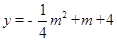 ,即可求出二次函数的表达式;
,即可求出二次函数的表达式; (x-2)2+1,
(x-2)2+1, (x-2)2+1,得:y=2,
(x-2)2+1,得:y=2, m2+m),点B(0,m),
m2+m),点B(0,m), m2+m)=
m2+m)= m2,
m2,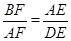 ,
,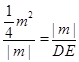 ,
, m2+m),
m2+m), m2+m+4),
m2+m+4), m2+m+4,
m2+m+4, •(
•(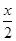 )2+
)2+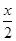 +4,
+4, x2+
x2+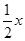 +4,
+4,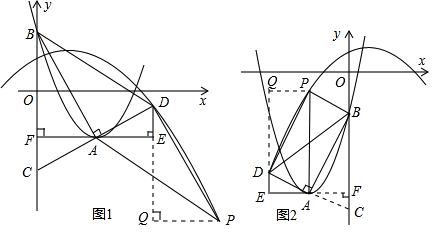
 m2+m+4)-(
m2+m+4)-( m2)=-
m2)=- m2+m+4,
m2+m+4, m2+m+4)的坐标代入y=-
m2+m+4)的坐标代入y=- x2+
x2+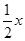 +4得:-
+4得:- m2+m+4=-
m2+m+4=- ×(3m)2+
×(3m)2+ ×(3m)+4,
×(3m)+4, m2+m+4)+(
m2+m+4)+( m2)=m+4,
m2)=m+4, x2+
x2+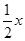 +4得:
+4得: m2+
m2+ m+4,
m+4,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com