
【题目】如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.求点C到AB的距离. 
【答案】解:在AB上截取AE=AC=3,连接CE,过C作CF⊥AB于F点. 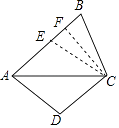
∵AC平分∠BAD,
∴∠BAC=∠DAC.
在△ADC与△AEC中,
∵ 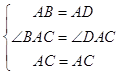 ,
,
∴△ADC≌△AEC(SAS),
∴CE=CD.
∵CD=CB,
∴CE=CB.
∵CF⊥BE,
∴CF垂直平分BE.
∵AB=5,
∴BE=2,
∴EF=1,
∴AF=4,
在Rt△ACF中,
∵CF2=AC2﹣AF2=52﹣42=9,
∴CF=3.
【解析】在AB上截取AE=AC=3,连接CE,过C作CF⊥AB于F点,根据SAS定理得出△ADC≌△AEC,故可得出CE=CD,再由垂直平分线的性质求出AF的长,根据勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 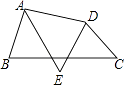
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒. 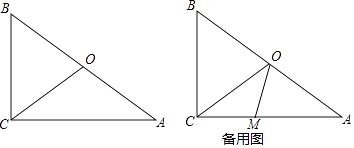
(1)当∠AMO=∠AOM时,求t的值;
(2)当△COM是等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电厂有5000吨电煤.
(1)求:这些电煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批电煤能用多少天?
(3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用电煤300吨,则这批电煤共可用多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
查看答案和解析>>
科目:初中数学 来源: 题型:
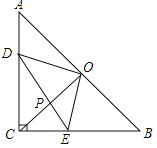
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com