
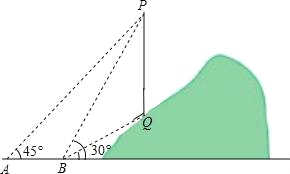
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.
【答案】6+2![]() 米.
米.
【解析】
试题分析:延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
试题解析:延长PQ交直线AB于点E,设PE=x米.
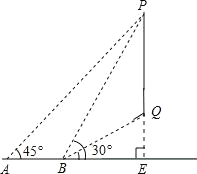
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x米,
x米,
∵AB=AE-BE=6米,
则x-![]() x=6,
x=6,
解得:x=9+3![]() .
.
则BE=(3![]() +3)米.
+3)米.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=(3+
+3)=(3+![]() )米.
)米.
∴PQ=PE-QE=9+3![]() -(3+
-(3+![]() )=6+2
)=6+2![]() (米).
(米).
答:电线杆PQ的高度是6+2![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】已知两个有理数的和比其中任何一个加数都小 ,那么一定是 ( )
A. 这两个有理数同为正数 B. 这两个有理数同为负数
C. 这两个有理数异号 D. 这两个有理数中有一个为零
查看答案和解析>>
科目:初中数学 来源: 题型:
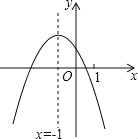
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac-b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,从左到右的变形是因式分解的是( )
A.(x+3y)(x﹣3y)=x2﹣9y2
B.a(x+y+1)=ax+ay+a
C.4x2﹣1=(2x+1)(2x﹣1)
D.a2c﹣a2b+1=a2(c﹣b)+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com