已知关于x的方程(a+c)x2+2bx-(c-a)=0的两根之和为-1,两根之差为1,其中a,b,c是△ABC的三边长.
(1)求方程的根;(2)试判断△ABC的形状.
解:(1)设方程的两根为x
1,x
2(x
1>x
2),
则x
1+x
2=-1①,x
1-x
2=1②,
①+②得2x
1=0,解得x
1=0,
①-②得:2x
2=-2,解得x
2=-1;
(2)∵x
1+x
2=-1=-
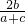
,x
1x
2=
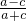
=0,
∴a-c=0,2b=a+c,
∴a=c,2b=2a=2c,
综上可知:a=c=b,
所以△ABC为应为等边三角形.
分析:(1)先根据题意,列出关于x
1,x
2的二元一次方程组,可以求出方程的两个根0和-1;
(2)然后把所求两根代入原方程,判断a、b、c的关系,最后确定三角形的形状.
点评:本题综合考查了三角形形状的判断与根与系数的关系,解这类题的关键是利用根与系数的关系,用方程根的定义来寻求未知系数的等量关系.

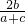 ,x1x2=
,x1x2=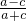 =0,
=0,
