
| A、sinα>cosα | B、sinα<cosα | C、sinα=cosα | D、以上三种都有可能 |
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年浙江省湖州市八年级上学期期中考试数学卷 题型:解答题
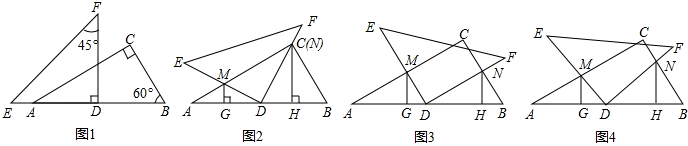
已知:将一副三角板(Rt△ABC和Rt△DEF)如图①摆放,点E、A、D、B在一条直线上,且D是AB的中点。将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE、AC相交于点M,直线DF、BC相交于点N,分别过点M、N作直线AB的垂线,垂足为G、H.
1.当α=30°时,DF刚好过点C(如图②),求证:AM=DM;
2.在(1)的条件下,试判断线段AG与DH的数量关系,并说明理由;
3.“当在Rt△DEF绕点D顺时针方向旋转过程中时α=60°(如图③),(2)中的结论是否成立?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com