
分析 (1)原式去括号合并即可得到结果;
(2)原式第一项利用乘方的意义化简,第二项利用绝对值的代数意义化简,最后一项利用算术平方根定义计算即可得到结果;
(3)方程变形后,利用平方根定义开方即可求出解;
(4)方程变形后,利用立方根定义开立方即可求出解.
解答 解:(1)原式=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{2}$=$\sqrt{3}$;
(2)原式=9-$\frac{1}{2}$+$\frac{1}{2}$-3=6;
(3)方程变形得:x2=121,
开方得:x=±11;
(4)方程变形得:(x-5)3=-8,
开立方得:x-5=-2,
解得:x=3.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
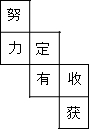 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )| A. | 定 | B. | 有 | C. | 收 | D. | 获 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,在中间长为(a+b)的正方形空地上将修建一座雕像,规划部门计划将阴影部分进行绿化,则绿化的面积是多少平方米?并求出当a=5,b=3时的绿化面积.
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,在中间长为(a+b)的正方形空地上将修建一座雕像,规划部门计划将阴影部分进行绿化,则绿化的面积是多少平方米?并求出当a=5,b=3时的绿化面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)和(3) | B. | (2)和(4) | C. | (3)和(4) | D. | 1)和(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=b | B. | a=c | C. | a=2b=c | D. | b=c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com