
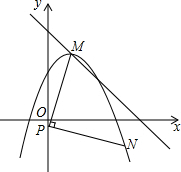
 已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标.
已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标. 分析 由抛物线的顶点式求得M的坐标,作ME⊥y轴于E,NF⊥y轴于F,根据已知得出∠PME=∠NPF,然后证得△PME≌△NPF,得出FN=PE,PF=ME,设P(0,n),则PE=FN=3-n,PF=EM=1,得出N(3-n,n-1),代入抛物线的解析式即可求得.
解答 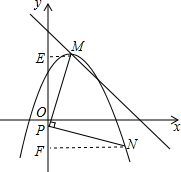 解:∵抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,
解:∵抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,
∴M(1,3),
作ME⊥y轴于E,NF⊥y轴于F,
∵PN⊥PM,
∴∠MPE+∠NPF=90°,
∵∠MPE+∠PME=90°,
∴∠PME=∠NPF,
在△PME和△NPF中,
$\left\{\begin{array}{l}{∠PME=∠NPF}\\{∠PEM=∠NFP}\\{PM=PN}\end{array}\right.$,
∴△PME≌△NPF(AAS),
∴FN=PE,PF=ME,
设P(0,n),则PE=FN=3-n,PF=EM=1,
∴N(3-n,n-1),
∵点N在抛物线上,
∴n-1=-$\frac{3}{4}$(3-n-1)2+3
解得n=$\frac{2}{3}$或n=2,
∴P(0,$\frac{2}{3}$)或(0,2).
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征,等腰直角三角形的性质,三角形全等的判定和性质,作出辅助线构建全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )
如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )| A. | (-1,1) | B. | (-1,2) | C. | (-2,1) | D. | (-2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
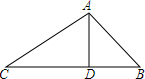 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
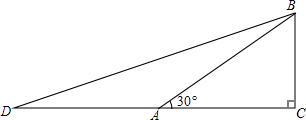 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com