
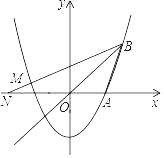
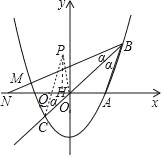
【题目】如图,抛物线y=![]() x2+bx+c过点A(2,0)和B(3,3).
x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
【答案】(1)![]() ;(2)①ON=6;②点P坐标为
;(2)①ON=6;②点P坐标为![]() 或
或![]()
【解析】
(1)把点A、B坐标代入二次函数表达式,即可求解;
(2)①证明△BOL≌△BOA,利用![]() 即可求解;②当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,分别求解即可.
即可求解;②当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,分别求解即可.
解:(1)把点A、B坐标代入二次函数表达式:
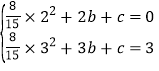 ,解得:
,解得: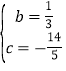 ,
,
故:抛物线的表达式为:![]() ……①;
……①;
(2)①过点B分别向x轴、y轴作垂线,交于点S、K,连接A、L,
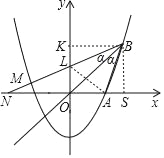
点B坐标为(3,3)则:四边形OSBK为正方形,
∵∠MBO=∠ABO,BO是正方形OSBK的对角线,BO=BO,
∴△BOL≌△BOA(AAS),
∴OA=OL=2,∴AL⊥BO,
sinα=![]() =
=![]() =
=![]() ,则cosα=
,则cosα=![]() ,tanα=
,tanα=![]() ,
,
∵OL∥BS,∴![]() ,即:
,即:![]() ,
,
则:ON=6;
②则点N坐标为(﹣6,0),
把点L(0,2)、N坐标代入一次函数表达式:y=kx+b,
解得:y=![]() x+2…②,
x+2…②,
联立①、②解得:x=﹣3或3(舍去3)
即点M坐标为(﹣3,1),
BC所在的直线的表达式为:y=x…③,
联立①、③解得:x=﹣![]() 或3(舍去3),
或3(舍去3),
则点C坐标为(﹣![]() ,﹣
,﹣![]() ),
),
则:OM=![]() ,OB=3
,OB=3![]() ,OC=
,OC=![]() ,MB=2
,MB=2![]()
当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,
当点P在第二象限时,如下图,过点P作PH⊥x轴,
△POC∽△MOB,∠PCO=∠MBO=α,
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
解得:OP=![]()
![]() ,PC═
,PC═![]() ,
,
AB所在直线表达式中的k值为3,
∵∠PCO=∠MBO=∠OBA=α,
∴PC所在直线表达式中的k值为3,
则:PC所在的直线表达式为:y=3x+![]() ,
,
令y=0,则x=﹣![]() ,
,
即Q点坐标为(﹣![]() ,0),即:OQ=
,0),即:OQ=![]() ,
,
则:CQ=![]()
![]() ,则:PQ=PC﹣CQ,
,则:PQ=PC﹣CQ,
而PH2=OP2﹣OH2=PQ2﹣QH2=PQ2﹣(OQ﹣OH)2,
其中,OP=![]()
![]() ,PQ=PC﹣CQ,OQ=
,PQ=PC﹣CQ,OQ=![]() ,
,
解得:OH=![]() ,
,
则点P坐标为(﹣![]() ,
,![]() ),
),
当点P在第四象限时,同理可求点P坐标为![]() ,
,
故点P坐标为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
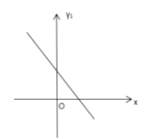
【题目】在平面直角坐标系中,函数y1=ax+b(a、b为常数,且ab≠0)的图象如图所示,y2=bx+a,设y=y1·y2.
(1)当b=-2a时,
①若点(1,4)在函数y的图象上,求函数y的表达式;
②若点(x1,p)和(x2,q)在函数y的图象上,且![]() ,比较p,q的大小;
,比较p,q的大小;
(2)若函数y的图象与x轴交于(m,0)和(n,0)两点,求证:m=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
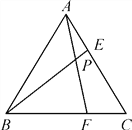
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
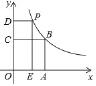
【题目】如图,在平面直角坐标系中,面积为4的正方形![]() 的顶点
的顶点![]() 与坐标原点重合,边
与坐标原点重合,边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 、
、![]() 都在函数
都在函数![]() 的图象上,过动点
的图象上,过动点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线,交
轴的平行线,交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() .设矩形
.设矩形![]() 与正方形
与正方形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的横坐标为m.
的横坐标为m.
(1)求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年大唐芙蓉园新春灯会以“鼓舞中华”为主题,既有新年韵味,又结合“一带一路”展示了丝绸之路上古今文化经贸繁荣的盛况。小丽的爸爸买了两张门票,她和各个两人都想去观看,可是爸爸只能带一人去,于是读九年级的哥哥提议用他们3人吃饭的彩色筷子做游戏(筷子除颜色不同,其余均相同),其中小丽的筷子颜色是红色,哥哥的是银色,爸爸的是白色,将3人的3双款子全部放在 一个不透明的筷篓里摇匀,小丽随机从筷篓里取出一根,记下颜色放回,然后哥哥同样从筷篓里取出一根,若两人取出的筷子颜色相同则小丽去,若不同,则哥哥去。
(1)求小丽随机取出一根筷子是红色的概率;
(2)请用列表或画树状图的方法求出小随爸爸去看新春灯会的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
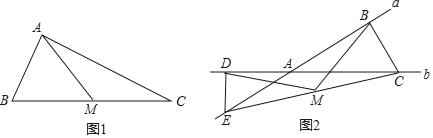
【题目】(1)如图1,在△ABC中,点M为BC边的中点,且MA=![]() BC,求证:∠BAC=90°.
BC,求证:∠BAC=90°.
(2)如图2,直线a、b相交于点A,点C、E分别是直线b、a上两点,ED⊥b,垂足为点D,点M是EC的中点,MD=MB,DE=2,BC=3,求△ADE和△ABC的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com