
| 4400 |
| x+1.2x |
| 4400 |
| x |
| 4400 |
| x+1.2x |
| 4400 |
| x |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
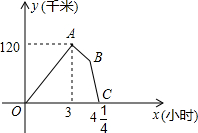 离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•黄冈模拟)如图所示,有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字.分别转动转盘A、B,待两个转盘都停止后,将两个指针所指份内的数字分别记作m和n(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).将m和n分别记作点P的横坐标与纵坐标,那么点P(m,n)在函数y=2x的图象上的概率是多少?(用树状图或列表法表示)
(2012•黄冈模拟)如图所示,有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字.分别转动转盘A、B,待两个转盘都停止后,将两个指针所指份内的数字分别记作m和n(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).将m和n分别记作点P的横坐标与纵坐标,那么点P(m,n)在函数y=2x的图象上的概率是多少?(用树状图或列表法表示)查看答案和解析>>
科目:初中数学 来源: 题型:
|
 公司确定国内、国外市场的销量各为多少万辆时,该公司的年利润最大?
公司确定国内、国外市场的销量各为多少万辆时,该公司的年利润最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com