
【题目】为了解嘉峪关初三学生体育测试自选项目的情况,从我市初三学生中随机抽取中部分学生的自选项目进行统计,绘制了扇形统计图和频数分布直方图,请根据图中信息,回答下列问题: 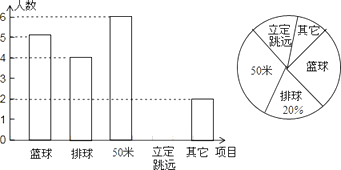
(1)本次调查共抽取了名学生;
(2)此次调查报其他项目的人数占了(填百分数),报立定跳远的人数是;
(3)扇形统计图中50米部分所对应的圆心角的度数是;
(4)我市共有初三学生3000名,估计我市有多少名学生选报篮球项目?
【答案】
(1)20
(2)10%;3
(3)108°
(4)解:3000× ![]() =750,
=750,
答:估计我市有750名学生选报篮球项目
【解析】解:(1)本次调查共抽取的学生数为4÷20%=20人; 所以答案是:20;(2)此次调查报其他项目的人数占了 ![]() ×100%=10%,报立定跳远的人数是:20﹣5﹣4﹣6﹣2=3人,
×100%=10%,报立定跳远的人数是:20﹣5﹣4﹣6﹣2=3人,
所以答案是:10%,3;(3)扇形统计图中50米部分所对应的圆心角的度数是:360°× ![]() =108°,
=108°,
所以答案是:108°;
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图),以及对扇形统计图的理解,了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点. 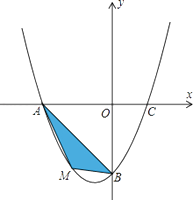
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:

(1)放入一个小球水面升高 ,![]() ,放入一个大球水面升高
,放入一个大球水面升高 ![]() ;
;
(2)如果要使水面上升到50![]() ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分别标有数字1、﹣2、﹣3、4,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.
(1)求小芳抽到负数的概率;
(2)若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB. 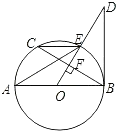
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是边长分别为4 ![]() 和2的两个等边三角形纸片ABC和OD′E′叠放在一起(C与O重合).
和2的两个等边三角形纸片ABC和OD′E′叠放在一起(C与O重合). 
(1)操作:固定△ABC,将△ODE绕点C顺时针旋转30°,后得到△ODE,连接AD、BE、CE的延长线交AB于F(图2): 探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)在(1)的条件下将△ODE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR,当点P与点F重合时停止运动(图3). 探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)将图1中△ODE固定,把△ABC沿着OE方向平移,使顶点C落在OE的中点G处,设为△ABG,然后奖△ABG绕点G顺时针旋转,边BG交边DE于点M,边AG交边DO于点N,设∠BGE=α(30°<α<90°)(图4). 探究:在图4中,线段ONEM的值是否随α的变化而变化?如果没有变化,请你求出ONEM的值,如果有变化,请你说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).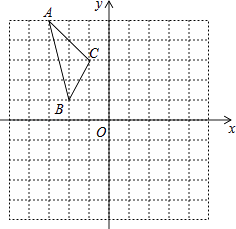
(1)若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com