
【题目】你会求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ,
,
![]() ,
,
![]() ,
,
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
【答案】(1)a2015﹣1;(2)22015﹣1;(3)![]() .
.
【解析】
(1)根据已知算式得出规律,即可得出答案.
(2)先变形,再根据规律得出答案即可.
(3)先变形,再根据规律得出答案即可.
(1)由上面的规律我们可以大胆猜想,(a﹣1)(a2012+a2011+a2010+…+a2+a+1)=a2015﹣1,
故答案为:a2015﹣1;
(2)22014+22013+22012+…+22+2+1
=(2﹣1)×(22014+22013+22012+…+22+2+1)
=22015﹣1,
故答案为:22015﹣1;
(3)52014+52013+52012+…+52+5+1
=![]() ×(5﹣1)×(52014+52013+52012+…+52+5+1)
×(5﹣1)×(52014+52013+52012+…+52+5+1)
=![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( ) 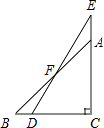
A.10°
B.15°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细观察,找规律
下列各图中的MA1与NAn平行.

(1)图①中的∠A1+∠A2= ______ 度,
图②中的∠A1+∠A2+∠A3= ______ 度,
图③中的∠A1+∠A2+∠A3+∠A4= ______ 度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= ______ 度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= ______ 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1= ______
(3)请你证明图②的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.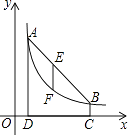
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF= ![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
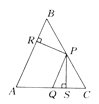
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
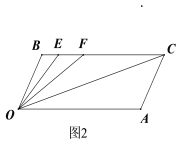
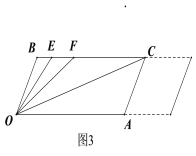
【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
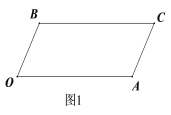
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图: 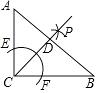
①以C为圆心,以适当长为半径画弧交AC于E,交BC于F.
②分别以E,F为圆心,以大于 ![]() EF的长为半径作弧,两弧相交于P;
EF的长为半径作弧,两弧相交于P;
③作射线CP交AB于点D,
若AC=3,BC=4,则△ACD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
已知:如图,![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.
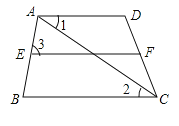
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() .
.
∴![]() ,( )
,( )
又∵![]() ,(已知)
,(已知)
∴______![]() ,(内错角相等,两直线平行)
,(内错角相等,两直线平行)
∴![]() _______,( )
_______,( )
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt△ABQ,使∠BAQ=90°,tan∠ABQ= ![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.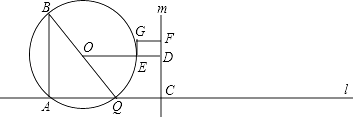
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com