
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,8),(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A'处,折痕所在直线交y轴正半轴于点C.

(1)求直线BC的函数表达式;
(2)把直线BC向左平移,使之经过点A',求平移后直线的函数表达式.
【答案】(1)y=﹣![]() x+3;(2)y=﹣
x+3;(2)y=﹣![]() x﹣2.
x﹣2.
【解析】
(1)在Rt△OAB中,OA=8,OB=6,用勾股定理计算出AB=10,再根据折叠的性质得BA′=BA=10,CA′=CA,则OA′=BA′﹣OB=4,设OC=t,则CA=CA′=8﹣t,在Rt△OA′C中,根据勾股定理得到t2+42=(8﹣t)2,解得t=3,则C点坐标为(0,3),然后利用待定系数法确定直线BC的函数表达式即可;
(2)由(1)可知点A′的坐标为(﹣4,0),根据平移的性质可设平移后的直线为y=﹣![]() x+m,再将(﹣4,0)代入即可求得平移后直线的函数表达式.
x+m,再将(﹣4,0)代入即可求得平移后直线的函数表达式.
解:(1)∵A(0,8),B(6,0),
∴OA=8,OB=6,
在Rt△OAB中,AB=![]() =10.
=10.
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=10,CA′=CA,
∴OA′=BA′﹣OB=10﹣6=4.
设OC=t,则CA=CA′=8﹣t,
在Rt△OA′C中,∵OC2+OA′2=CA′2,
∴t2+42=(8﹣t)2,解得t=3,
∴C点坐标为(0,3),
设直线BC的解析式为y=kx+b,
把B(6,0)、C(0,3)代入
得![]() ,解得
,解得 ,
,
∴直线BC的解析式为y=﹣![]() x+3;
x+3;
(2)∵OA′=4,
∴点A′的坐标为(﹣4,0)
∵把直线BC向左平移,使之经过点A',
∴设平移后直线的函数表达式为y=﹣![]() x+m,
x+m,
将(﹣4,0)代入,得
0=2+m,
解得m=﹣2,
∴平移后直线的函数表达式为y=﹣![]() x﹣2.
x﹣2.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,
∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别为多少?

(2)(生活应用题)某公司对一批某一品牌的衬衣的质量抽检结果如下表:

①从这批衬衣中任抽1件是次品的概率约为多少?
②如果销售这批衬衣600件,那么至少需要准备多少件正品衬衣供买到次品的顾客调换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质,下面是探究过程,请补充完整:
的图象与性质,下面是探究过程,请补充完整:
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数![]() 的自变量
的自变量![]() 的取值范围是__________,
的取值范围是__________, ![]() 的值为__________.
的值为__________.
(![]() )描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
)描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
(![]() )进一步探究函数图象发现:
)进一步探究函数图象发现:
①函数图象与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有__________个实数根.
有__________个实数根.
②方程![]() 有__________个实数根.
有__________个实数根.
③结合函数的图象,写出该函数的一条性质__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
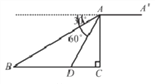
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com