练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知关于x的一元二次方程x2-x-3=0的两个实数根分别是α，β；则（α+1）（β+1）=-1．

    分析 由根与系数的关系可得出α+β=1、αβ=-3，将其代入（α+1）（β+1）=αβ+（α+β）+1中即可求出结论．

    解答 解：∵方程x2-x-3=0的两个实数根分别是α，β，
    ∴α+β=1，αβ=-3，
    ∴（α+1）（β+1）=αβ+（α+β）+1=-3+1+1=-1．
    故答案为：-1．

    点评 本题考查了根与系数的关系，根据根与系数的关系找出α+β=1、αβ=-3是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

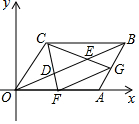    12．如图，平面直角坐标系中O是原点，?ABCD的顶点A，C的坐标分别是（8，0），（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB于点F，G，连接FG．则下列结论：
    ①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是$\frac{20}{3}$；④OD=$\frac{4\sqrt{5}}{3}$
    其中正确的结论是①③（填写所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

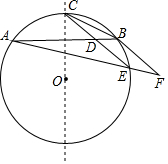    13．如图示AB为⊙O的一条弦，点C为劣弧AB的中点，E为优弧AB上一点，点F在AE的延长线上，且BE=EF，线段CE交弦AB于点D．
    ①求证：CE∥BF；  
    ②若BD=2，且EA：EB：EC=3：1：$\sqrt{5}$，求△BCD的面积（注：根据圆的对称性可知OC⊥AB）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在⊙O 中，已知∠AOB=120°，则∠ACB=60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，抛物线y=$\frac{2}{3}$x2+bx+c经过点B（3，0），C（0，-2），直线l：y=-$\frac{2}{3}$x-$\frac{2}{3}$交y轴于点E，且与抛物线交于A，D两点，P为抛物线上一动点（不与A，D重合）．
    （1）求抛物线的解析式；
    （2）当点P在直线l下方时，过点P作PM∥x轴交l于点M，PN∥y轴交l于点N，求PM+PN的最大值．
    （3）设F为直线l上的点，以E，C，P，F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知四边形ABCD的一组对边AD、BC的延长线交于点E．
    （1）如图1，若∠ABC=∠ADC=90°，求证：ED•EA=EC•EB；
    （2）如图2，若∠ABC=120°，cos∠ADC=$\frac{3}{5}$，CD=5，AB=12，△CDE的面积为6，求四边形ABCD的面积；
    （3）如图3，另一组对边AB、DC的延长线相交于点F．若cos∠ABC=cos∠ADC=$\frac{3}{5}$，CD=5，CF=ED=n，直接写出AD的长（用含n的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．我市东坡实验中学准备开展“阳光体育活动”，决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了m名学生（每名学生必选且只能选择这五项活动中的一种）．

    根据以上统计图提供的信息，请解答下列问题：
    （1）m=100，n=5．
    （2）补全上图中的条形统计图．
    （3）若全校共有2000名学生，请求出该校约有多少名学生喜爱打乒乓球．
    （4）在抽查的m名学生中，有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动，学校打算从小薇、小燕、小红、小梅这4名女生中，选取2名参加全市中学生女子羽毛球比赛，请用列表法或画树状图法，求同时选中小红、小燕的概率．（解答过程中，可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表）

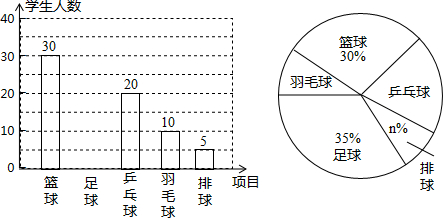
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．某同学用剪刀沿直线将一片平整的银杏叶减掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（　　）
    A．两点之间线段最短
    B．两点确定一条直线
    C．垂线段最短
    D．经过直线外一点，有且只有一条直线与这条直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法正确的是（　　）
    A．调查孝感区居民对创建“全国卫生城市”的知晓度，宜采用抽样调查
    B．一组数据85，95，90，95，95，90，90，80，95，90的众数为95
    C．“打开电视，正在播放乒乓球比赛”是必然事件
    D．同时抛掷两枚质地均匀的硬币一次，出现两个正面朝上的概率为$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案