
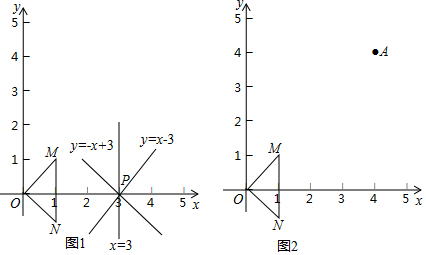
分析 (1)根据经过某点且平行于OM、ON或MN的直线,叫该点关于△OMN的“关联线”,可得答案;
(2)根据关联点,可得关于n,m的关系,根据图象上的点满足函数解析式,可得关于m,n的方程,根据解方程,可得答案;
(3)根据翻折的性质,可得OC′=OC=4,根据直角三角形的性质,可得∠C′OH的度数,根据正切函数,可得PH,根据线段的和差,可得平移的距离.
解答 解:(1)是点(4,3)关于△OMN的“关联线”,①x=4;③y=x-1.
①③.
(2)∵抛物线的顶点B(m,n)有一条关于△OMN的关联线是y=-x+5,
∴-m+5=n.
又∵抛物线过点A(4,4),或
∴$4=\frac{1}{4}{(4-m)^2}+n$.
联立,得$\left\{\begin{array}{l}{-m+5=n}\\{\frac{1}{4}(4-m)^{2}+n=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}m=2\\ n=3.\end{array}\right.$或$\left\{\begin{array}{l}m=10\\ n=-5.\end{array}\right.$
∵顶点B在第一象限,
∴$\left\{\begin{array}{l}m=2\\ n=3.\end{array}\right.$
∴抛物线的表达式为$y=\frac{1}{4}{(x-2)^2}+3$.
(3)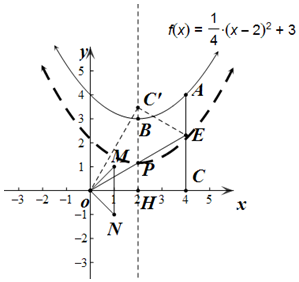 ,
,
由y=$\frac{1}{4}$(x-2)2+3,得顶点B(2,3).
将△OCE沿着OE折叠,点C落在点C′的位置,得
OC′=OC=4,∠C′OP=∠COP,OH=2.
∴∠C′OH=60°.
∴∠C′OP=∠COP=30°.
∴PH=$OH•tan30°=2×\frac{{\sqrt{3}}}{3}=\frac{{2\sqrt{3}}}{3}$.
∴抛物线需要向下平移的距离
BP=BH-PH=$3-\frac{{2\sqrt{3}}}{3}$=$\frac{{9-2\sqrt{3}}}{3}$.
条件的抛物线沿对称轴向下平移$\frac{9-2\sqrt{3}}{3}$距离,其顶点落在OE上.
点评 本题考查了二次函数综合题,解(1)的关键是关联线的定义;解(2)的关键是利用关联线,图象上的点满足函数解析式得出方程组;解(3)的关键是利用翻折的性质得出OC′=OC=4,∠C′OP=∠COP,又利用了直角三角形的性质,锐角正切函数.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:解答题
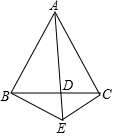 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.
如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k<2 | C. | 0<k<2 | D. | -2<k<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
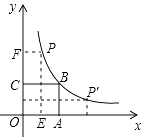 如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
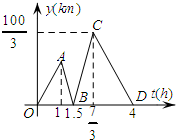 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
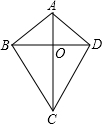 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com