
 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:分析 ①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;
②由AE=EF<BE,可得AD>2AE,在用锐角三角函数即可判断;
③由AG=GF>OG,可得△AGD的面积>△OGD的面积;
④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;
⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG;
⑥根据四边形AEFG是菱形可知AB∥GF,AB=GF,再由∠BAO=45°,∠GOF=90°可得出△OGF时等腰直角三角形,由S△OGF=1求出GF的长,进而可得出BE及AE的长,利用正方形的面积公式可得出结论.
解答 解:∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG=$\frac{1}{2}$∠ADO=22.5°,故①正确.
∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE<$\frac{1}{2}$AB,
∴$\frac{AD}{AE}$>2,
在Rt△ADE中,tan∠AED=$\frac{AD}{AE}$>2,故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,故④正确.
∴∠OGF=∠OAB=45°,
∴EF=GF=$\sqrt{2}$OG,
∴BE=$\sqrt{2}$EF=$\sqrt{2}$×$\sqrt{2}$OG=2OG.故⑤正确.
∵四边形AEFG是菱形,
∴AB∥GF,AB=GF.
∵∠BAO=45°,∠GOF=90°,
∴△OGF时等腰直角三角形.
∵S△OGF=1,
∴$\frac{1}{2}$OG2=1,解得OG=$\sqrt{2}$,
∴BE=2OG=2$\sqrt{2}$,GF=$\sqrt{2+2}$═2,
∴AE=GF=2,
∴AB=BE+AE=2$\sqrt{2}$+2,
∴S正方形ABCD=AB2=(2$\sqrt{2}$+2)2=12+8$\sqrt{2}$,故⑥错误.
∴其中正确结论的序号是:①④⑤共三个.
故答案为①④⑤.
点评 此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质、锐角三角函数等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
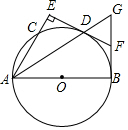 如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.
如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
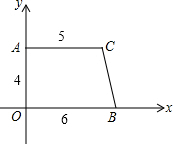 如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
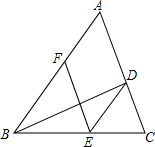 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
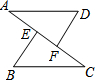 如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.
如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
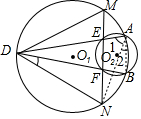 如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)
如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
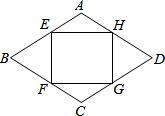 如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,
如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 顶点坐标是(1,2) | ||
| C. | 与y轴交点坐标为(0,2) | D. | 与x轴有两个交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com