
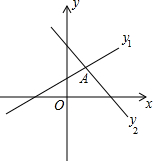
 如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.
如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 24km/h,8km/h | B. | 22.5km/h,2.5km/h | ||
| C. | 18km/h,24km/h | D. | 12.5km/h,1.5km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
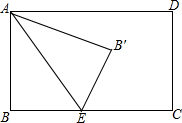 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )
如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )| A. | 1或2 | B. | 2或3 | C. | 3或4 | D. | 4或5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
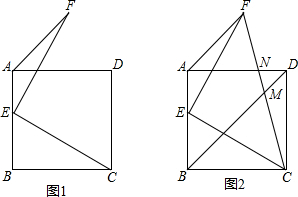 如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
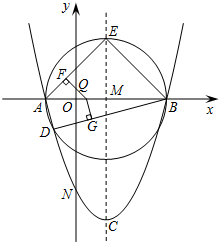 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com