
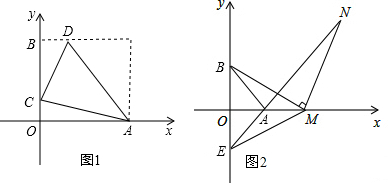
分析 (1)根据非负数的性质求得a、b的值,则易求点A、B的坐标;
(2)如图1,连接AC,过点D作DF⊥AB于点F,构建相似三角形(△ACO∽△ADF),利用相似三角形的性质,勾股定理来求BD的长度,即点D的横坐标即可;
(3)如图2,连接BN,作NF⊥OA于F,思想利用四点共圆证明△BMN是等腰直角三角形,再证明△BMO≌△MNF得NF=MO,MF=BO=12,设点M(m,0),列出方程解决.
解答 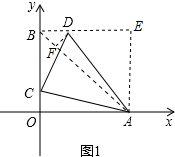 解:(1)∵$\sqrt{a-b}$+|2a-3b+4|=0,
解:(1)∵$\sqrt{a-b}$+|2a-3b+4|=0,
∴$\left\{\begin{array}{l}{a-b=0}\\{2a-3b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=4}\\{b=4}\end{array}\right.$,
则A(4,0),B(0,4);
(2)如图1,连接AC,过点D作DF⊥AB于点F,
∵四边形OAEB是正方形,
∴∠OAB=45°,
又∵∠DAC=45°,
∴∠OAC=∠FAD.
又∵∠AOC=∠FAD=90°,
∴△ACO∽△ADF,
∴$\frac{OC}{DF}$=$\frac{OA}{FA}$,即$\frac{1}{DF}$=$\frac{4}{FA}$,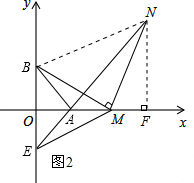
∴FA=4DF.
设DF=a,则FA=4a.
∴在等腰直角△DFB中,易求BD=$\sqrt{2}$a,
∴DE=4-$\sqrt{2}$a,
∴AD2=FA2+DF2=DE2+AE2,即16a2+a2=(4-$\sqrt{2}$a)2+42,
解得a1=-$\frac{4\sqrt{2}}{3}$(舍去),a2=$\frac{4\sqrt{2}}{5}$,
∴BD=$\sqrt{2}$a=$\frac{8}{5}$,
故B($\frac{8}{5}$,4);
(3)如图2,连接BN,作NF⊥OA于F.
∵OA=OE=OB=12,∠BOA=∠AOE=90°,
∴∠BAO=∠ABO=∠OAE=∠OEA=45°,
∴∠EAB=∠BAN=90°,
∵∠BAN=∠BMN=90°,
∴四边形BAMN四点共圆,
∴∠BAO=∠BNM=45°,
∴∠MBN=∠MNB=45°,
∴BM=MN,
∵∠BMO+∠NMF=90°,∠NMF+∠MNF=90°,
∴∠BMO=∠MNF,
在△BMO和△MNF中,
$\left\{\begin{array}{l}{∠BOM=∠MFN}\\{∠BMO=∠MNF}\\{BM=MN}\end{array}\right.$,
∴△BMO≌△MNF(AAS),
∴NF=MO,MF=BO=12,设点M(m,0),
∵S△AMN=$\frac{3}{2}$S△AME
∴$\frac{1}{2}$×(m-12)×m=$\frac{3}{2}$×$\frac{1}{2}$×(m-12)×12,
∴m=18,
∴点M坐标为(18,0).
点评 本题考查等腰三角形的性质、全等三角形的判定和性质、四点共圆等知识,解题的关键是添加辅助线构造全等三角形,利用特殊三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{270}{200+x}$=$\frac{330}{x}$ | B. | $\frac{270}{200-x}$=$\frac{330}{x}$ | C. | $\frac{270}{x}$=$\frac{330}{200+x}$ | D. | $\frac{270}{x}$=$\frac{330}{200-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
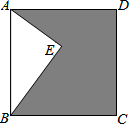 如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )
如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )| A. | 76 | B. | 24 | C. | 48 | D. | 88 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{x}$ | C. | $\root{3}{27}$ | D. | $\sqrt{{x}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
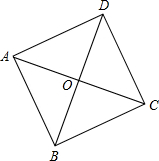 如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )| A. | AC=BD | B. | AB=BC | C. | ∠ABC=90° | D. | AO=BO |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com