
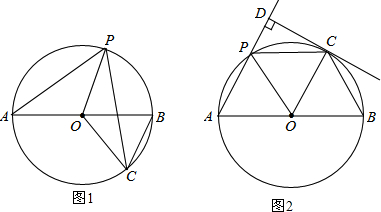
分析 (1)如图1,根据折叠的性质得∠1=∠2,加上∠A=∠1,则∠A=∠2,再根据圆周角定理得到∠A=∠3,所以∠2=∠3,于是可根据平行线的判定方法判断PO∥BC;
(2)如图2,根据直角三角形三边的关系,先由PC=2PD得到∠1=30°,∠2=60°,再利用折叠的性质得∠3=∠4,则利用平角的定义可计算出∠3=60°,从而判断△OPC为等边三角形,得到∠5=60°,所以∠OCD=90°,然后根据切线的判定定理可得CD是⊙O的切线.
解答 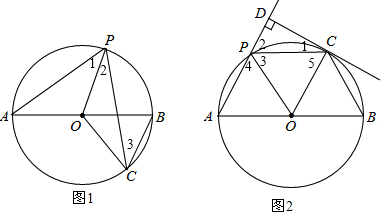 (1)解:PO∥BC.理由如下:如图1,
(1)解:PO∥BC.理由如下:如图1,
∵△AOP沿OP对折,点A的对应点C恰好落在⊙O上,
∴∠1=∠2,
又∵OA=OP,
∴∠A=∠1,
∴∠A=∠2,
∵∠A=∠3,
∴∠2=∠3,
∴PO∥BC;
(2)证明:如图2,
∵CD⊥直线AP,
∴∠PDC=90°
∵PC=2PD,
∴∠1=30°,
∴∠2=60°,
∵△AOP沿OP对折,点A的对应点C恰好落在⊙O上,
∴∠3=∠4,
∴∠3=$\frac{1}{2}$(180°-60°)=60°,
而OP=OC,
∴△OPC为等边三角形,
∴∠5=60°,
∴∠OCD=∠1+∠5=90°,
∴OC⊥CD,
∴CD是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了折叠的性质、圆周角定理和等边三角形的判定与性质.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
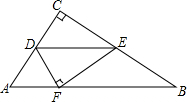 如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )| A. | 3.6 | B. | 4 | C. | 4.8 | D. | 6.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
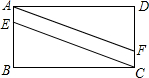 如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.
如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com