
【题目】如图,ABCD是圆O的内接四边形,BC是圆O的直径,∠ACB=20°,D为弧 ![]() 的中点,求∠DAC的度数.
的中点,求∠DAC的度数. 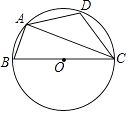
【答案】解:∵BC为圆O的直径,
∴∠BAC=90°,
∴∠B=90°﹣200=700 .
∵四边形ABCD为圆O内接四边形,
∴∠B+∠D=180°,
∴∠D=110°.
因为D为弧AC中点,
∴ ![]() =
= ![]() ,
,
∴∠DAC=35°
【解析】根据圆周角定理得到∠BAC=90°,求出∠B,根据圆内接四边形的性质求出∠D=110°,根据圆心角、弧、弦三者的关系定理解答即可.
【考点精析】掌握圆心角、弧、弦的关系和圆周角定理是解答本题的根本,需要知道在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,AD=a,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:DF=FE;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣9.8)﹣(+6);
(2)4.7﹣(﹣8.9)﹣7.5+(﹣6);
(3)1﹣3+5﹣7+9﹣11+…+97﹣99
(4)1.75+(﹣6![]() )+3
)+3![]() +(﹣1
+(﹣1![]() )+(+2
)+(+2![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D在BC边上,将△ABD绕点A按逆时针方向旋转得到△ACE,连接DE,则图中与∠BAD相等的角,除∠CAE外,还有角 . (用三个字母表示该角) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y= ![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(1)求这个二次函数的解析式;
(2)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(3)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com