

| AC |
| OC |
| AB |
| OP |
| AC |
| a+AC |
| h |
| l |
| ah |
| l-h |
| AB |
| OP |
| AC |
| OC |
| h |
| l |
| AC |
| OC-AC |
| h |
| l-h |
| AC |
| OA |
| h |
| l-h |
| h |
| l-h |
| h |
| l-h |
| h |
| l-h |
| hm |
| l-h |
 (3)根据题意设李华由A到A',身高为A'B',A'C'代表其影长(如图).
(3)根据题意设李华由A到A',身高为A'B',A'C'代表其影长(如图).| AC |
| OC |
| AB |
| OP |
| h |
| l |
| AC |
| OC |
| OA |
| OC |
| OC-AC |
| OC |
| l-h |
| l |
| OA′ |
| OC′ |
| l-h |
| l |
| OA |
| OC |
| OA′ |
| OC′ |
| AA′ |
| CC′ |
| OA′-OA |
| OC′-OC |
| l-h |
| l |
| AA′ |
| CC′ |
| v1 |
| v2 |
| l-h |
| l |
| lv1 |
| l-h |


科目:初中数学 来源: 题型:
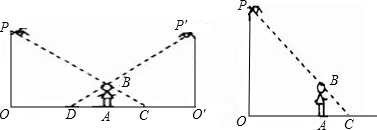
 如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.
如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.若李华距灯柱OP的水平距离OA=a,求他影子AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
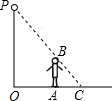 如图,李华晚上在路灯下散步,已知李华的身高AB=h,灯柱的高OP=l,李华距灯柱OP的水平距离OA=a.
如图,李华晚上在路灯下散步,已知李华的身高AB=h,灯柱的高OP=l,李华距灯柱OP的水平距离OA=a.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为
如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com