
科目:初中数学 来源: 题型:解答题
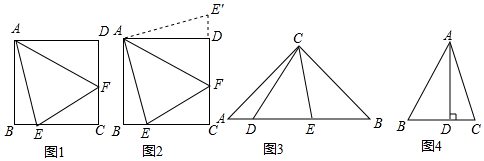
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
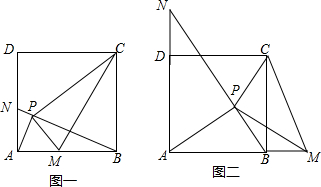
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
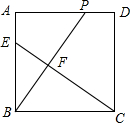 如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.
如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 周末,小军(用A表示),小明(用B表示),小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁边有四个座位,A先坐在如图所示的位置上,B,C,D三人随机坐到其他三个座位上,则A与B对面而坐的概率为$\frac{1}{3}$.
周末,小军(用A表示),小明(用B表示),小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁边有四个座位,A先坐在如图所示的位置上,B,C,D三人随机坐到其他三个座位上,则A与B对面而坐的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,C为⊙O上一点,AD垂直于过C点的直线,垂足为D,AC平分于∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD垂直于过C点的直线,垂足为D,AC平分于∠DAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com