Question

如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．

（1）求证：直线PA为⊙O的切线；

（2）试探究线段EF，OD，OP之间的等量关系，并加以证明；

（3）若BC＝6，tan∠F＝，求cos∠ACB的值和线段PE的长．

 

Answer 1

【答案】

（1）证明见解析；（2）EF²=4OD•OP，证明见解析；（3），.

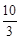【解析】

试题分析：（1）连接OB，根据垂径定理的知识，得出OA=OB，∠POA=∠POB，从而证明△PAO≌△PBO，然后利用全等三角形的性质结合切线的判定定理即可得出结论；

（2）先证明△OAD∽△OPA，由相似三角形的性质得出OA与OD、OP的关系，然后将EF=2OA代入关系式即可；

（3）根据题意可确定OD是△ABC的中位线，设AD=x，然后利用三角函数的知识表示出FD、OA，在Rt△AOD中，由勾股定理解出x的值，从而能求出cos∠ACB，再由（2）可得OA²=OD•OP，代入数据即可得出PE的长.

试题解析：（1）如图，连接OB，

∵PB是⊙O的切线，∴∠PBO=90°.

∵OA=OB，BA⊥PO于D，∴AD=BD，∠POA=∠POB.

又∵PO=PO，∴△PAO≌△PBO（SAS）.

∴∠PAO=∠PBO=90°. ∴直线PA为⊙O的切线.

（2）EF²=4OD•OP，证明如下：

∵∠PAO=∠PDA=90°，∴∠OAD+∠AOD=90°，∠OPA+∠AOP=90°.

∴∠OAD=∠OPA. ∴△OAD∽△OPA. ∴，即OA²=OD•OP.

又∵EF=2OA，∴EF²=4OD•OP.

（3）∵OA=OC，AD=BD，BC=6，∴OD=BC=3（三角形中位线定理）.

设AD=x，

∵tan∠F=，∴FD=2x，OA=OF=2x﹣3.

在Rt△AOD中，由勾股定理，得（2x﹣3）²=x²+3²，

解得，x₁=4，x₂=0（不合题意，舍去）.∴AD=4，OA=2x﹣3=5.

∵AC是⊙O直径，∴∠ABC=90°.

又∵AC=2OA=10，BC=6，∴cos∠ACB=.

∵OA²=OD•OP，∴3（PE+5）=25.∴PE=.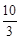

考点：1.切线的判定和性质；2.垂径定理；3.全等三角形的判定和性质；4.直角三角形两锐角的关系；5.相似三角形的判定和性质；6.三角形中位线定理；7.勾股定理；8.圆周角定理；9.锐角三角函数定义；10.特殊角的三角函数值.